Viewing COS Data¶
Learning Goals¶
This Notebook is designed to walk the user (you) through:
0. Introduction
- 0.1. A one-cell summary of this Notebook's key points
1. Reading in the data using Python
- 1.1. Investigating the Data - Basics
- 1.2. Reading in the x1d/x1dsum Main Data
- 1.3. The Association (asn) file
2. Displaying the data using common plotting techniques
- 2.1. Plotting an FUV Spectrum
2.1.1. Our First Plot
2.1.2. A Complex Look at the Entire FUV
2.1.3. Looking Closer at Parts of the FUV Spectrum
2.1.4. Reading and plotting the data with
specutils(optional)
- 2.2. Plotting an NUV Spectrum
3. Making a quick assessment of the data with tools to bin and measure the data's SNR and resolution
- 3.1. Understanding and Using Data Quality Flags
- 3.2. Binning the Data
3.2.1. Bringing in Some Useful Functions for Binning
3.2.2. Binning the FUV Data
- 3.3. Calculating the Signal-to-Noise Ratio
3.3.1. Defining a Useful Function for Estimating SNR
3.3.2. Choosing a Region to calculate SNR
3.3.3. Calculating the SNR
If you're confident with Reading-in and Plotting data in Python, you may run the first few cells defining directories and importing modules and then click the link when it appears to go ahead and skip to Section 3.
0. Introduction¶
The Cosmic Origins Spectrograph (COS) is an ultraviolet spectrograph on-board the Hubble Space Telescope (HST) with capabilities in the near ultraviolet (NUV) and far ultraviolet (FUV).
This tutorial aims to prepare you to begin analyzing COS data of your choice by walking you through reading and viewing a spectrum obtained with COS, as well as obtaining a few diagnostic measurements of your spectrum.
- For an in-depth manual to working with COS data and a discussion of caveats and user tips, see the COS Data Handbook.
- For a detailed overview of the COS instrument, see the COS Instrument Handbook.
0.1. A one-cell summary of this Notebook's key points:¶
While the rest of this Notebook will walk you through each step and decision made when examining your COS data, the following code cell serves as a summary for the Notebook. It contains the key material condensed into a single code cell, without much explanation. If this is all the help you need, great! If you still have questions, read on!
# This code cell condenses the key material of the Notebook into a single cell summary.
# 1. Import the necessary libraries:
from astropy.table import Table
from astropy.io import fits
from astroquery.mast import Observations
from cos_functions import estimate_snr
import matplotlib.pyplot as plt
# 2. Download an example dataset using astroquery:
# For more information, see the "Downloading your data" Notebook in this git repository
onecell_x1dsum_data_products = Observations.download_products(
Observations.filter_products(
Observations.get_product_list(
Observations.query_criteria(
obs_id="LDM701020" # The Obs ID of the observation to download
)
),
# Only downloads the 1 dimensional extracted spectrum
productSubGroupDescription="X1DSUM"
)
)
# 3. Read in the data to an Astropy Table:
x1dsum_data_table = Table.read(onecell_x1dsum_data_products["Local Path"][0])
# Some users may be familiar with another way to read in FITS table data, though it can be less user-friendly:
with fits.open(onecell_x1dsum_data_products["Local Path"][0]) as hdulist:
alternate_x1dsum_data_structure = hdulist[1].data
# 4. Estimate the S/N ratio of the spectrum by calculating sqrt(counts):
# The `estimate_snr` function is defined in the associated file: `cos_functions.py`
SNR_estimate = estimate_snr(x1dsum_data_table, binsize_=6, verbose=False)
# 5. Create a plot of the spectrum and the estimated S/N:
# Create 2-subplots and populate the upper one with the flux and the lower with S/N:
fig, (ax0, ax1) = plt.subplots(2, 1, figsize=(10, 8), sharex=True, dpi=100)
for i, segment_row in enumerate(x1dsum_data_table):
# In the upper panel, plot the spectrum as Flux over Wavelength:
ax0.plot(segment_row["WAVELENGTH"],
segment_row["FLUX"], label=f"Segment FUV{'AB'[i]}")
# In the lower panel, plot the S/N ratio as estimated S/N over Wavelength:
ax1.plot(SNR_estimate[1][i][0], SNR_estimate[1]
[i][1], label=f"Segment FUV{'AB'[i]}")
# Format the plot and save
ax0.legend()
# Adds a title of fontsize 20 points
ax0.set_title("Fig. 0.1\nSimple COS G160M Spectrum", size=20)
# Adds y axis label to the top panel
ax0.set_ylabel('Flux [$erg\ s^{-1}\ cm^{-2}\ Angstrom^{-1}$]', size=10)
# Adds y axis label to the bottom panel
ax1.set_ylabel(
'Estimated $\dfrac{SIGNAL}{NOISE}$ for a resolution element', size=10)
# Adds x axis label to the bottom panel
ax1.set_xlabel('Wavelength [$\AA$]', size=12)
plt.tight_layout()
plt.savefig("./Fig_0.1_quick_plot.png")
Now, returning to our more detailed walkthrough¶
Notes for those new to Python/Jupyter/Coding:¶
- You will frequently see exclamation points (!) or dollar signs (\$) at the beginning of a line of code we are telling you to run. These are not part of the actual commands. The exclamation points tell a jupyter Notebook to pass the following line to the command line, and the dollar sign merely indicates the start of a terminal prompt.
We will import the following packages:
numpyto handle array functions (version $\ge$ 1.17)pathlibfor managing system paths.astropy.io fitsfor accessing FITS filesastropy.table Tablefor creating tidy tables of the dataastropy.unitsandastropy.visualization.quantity_supportfor dealing with unitsmatplotlib.pyplotfor plotting dataastroquery.mast Observationsfor finding and downloading data from the MAST archive
Later on, we will import some functions from a local file, cos_functions.py, which is installed as part of the same GitHub repository as this Notebook. If you do not see this Python file in this directory, you can find it here. cos_functions.py must be installed next to this Notebook (ViewData.ipynb).
# Imports for: Downloading data from archive
from astroquery.mast import Observations
# Import for: Plotting
import matplotlib.pyplot as plt
# This line causes matplotlib plots to appear in the Notebook
# instead of possibly showing up in separate windows
%matplotlib inline
# Import for: Manipulating arrays
import numpy as np
# Import for: Managing system variables and paths
from pathlib import Path
# Imports for: Reading in data
from astropy.table import Table
from astropy.io import fits
# Imports for: Dealing with units and plotting them
from astropy.visualization import quantity_support
from astropy import units as u
quantity_support()
We will also define a few directories in which to place our data and plots, as well as a few colors we will use in plots later.
# These will be important directories for the Notebook
datadir = Path('./data')
outputsdir = Path('./output/')
plotsdir = Path('./output/plots')
# Make the directories if they don't exist
datadir.mkdir(exist_ok=True), outputsdir.mkdir(
exist_ok=True), plotsdir.mkdir(exist_ok=True)
# Specifying a few arbitrary colors to correspond to COS segments for plotting by their hex code
# Many search engines will show you the hex color - i.e. Google "#BC8C5B" to see this orange color
segment_colors = {'FUVA': '#BC8C5B', 'FUVB': '#4B6CA4',
'NUVA': '#1813CE', 'NUVB': '#61946E', 'NUVC': '#8C1A11'}
We will be working with some FUV and NUV datasets downloaded in the cell below.
These two datasets contain FUV observations of the QSO 3C48 and NUV observations of the Star WD1057 + 719, respectively.
Searching for and downloading data is out of the scope of this tutorial. If you wish to learn more, please see our tutorial on downloading COS data.
# Download the NUV data on WD1057+719 (with the G230L grating); only the _x1dsum and _asn
nuv_downloads = Observations.download_products(Observations.get_product_list(Observations.query_criteria(obs_id='lbbd01020')),
download_dir=str(datadir), extension='fits', mrp_only=True, cache=False)
# Download the FUV data on QSO 3C48; only the _x1dsum and _asn
fuv_downloads = Observations.download_products(Observations.get_product_list(Observations.query_criteria(obs_id='lcxv13050')),
download_dir=str(datadir), extension='fits', mrp_only=True, cache=False)
If you're confident Reading-in and Plotting data in Python, now go ahead to Section 3
1. Reading in the data¶
Calibrated COS 1-dimensional spectra are stored in fits files with the suffix x1d or x1dsum (1-dimensional here means that the cross-dispersion axis has been collapsed).
x1d files contain a spectrum processed from a single exposure, while x1dsum files contain summed data from multiple exposures at different fixed pattern noise position settings (FP-POS's). You may also encounter x1dsumN files, i.e. x1dsum1/x1dsum2/x1dsum3/x1dsum4, which are intermediate files containing data from multiple exposures at the same FP-POS. All of these files are sub-types of x1d files and thus share the same basic data structure. What you learn with one filetype is transferable to working with another.
We will be working with x1dsum files in this tutorial; however, please note that we often use the shorthand "x1d" as part of a variable name when programming, regardless of whether it is a summed file or not.
The calibrated spectrum data has been downloaded onto our local machine as: <current-working-directory>/data/mastDownload/HST/<Obs_id>/<Obs_id>_x1dsum.fits,
where the NUV and FUV Data are contained in the obs_ids:
| Spectral Region | Obs_id | Object Name | Object Type | filepath |
|---|---|---|---|---|
| FUV | LCXV13050 | QSO | 3C48 | ./data/mastDownload/HST/lcxv13050 |
| NUV | LBBD01020 | Star | WD1057 + 719 | ./data/mastDownload/HST/lbbd01020 |
1.1. Investigating the Data - Basics¶
We want to learn the basics about this file, then read in the data.
We can learn a great deal about our data from its primary fits header (see cell below).
# Make sure these filepath variables point to your new FUV data
# Note, We'll often refer to the x1dsum file with the prefix x1d for convenience
# However, the files are x1dsum files, not the related x1d files - more info in the Data Handbook
fuv_x1d_filepath = Path(
'./data/mastDownload/HST/lcxv13050/lcxv13050_x1dsum.fits')
# This is the association file, used for processing spectra with CalCOS:
fuv_asn_filepath = Path('./data/mastDownload/HST/lcxv13050/lcxv13050_asn.fits')
# Make sure these point to your new NUV data
nuv_x1d_filepath = Path(
'./data/mastDownload/HST/lbbd01020/lbbd01020_x1dsum.fits')
# This is the NUV association file
nuv_asn_filepath = Path('./data/mastDownload/HST/lbbd01020/lbbd01020_asn.fits')
nuv_x1d_header = fits.getheader(nuv_x1d_filepath)
nuv_asn_header = fits.getheader(nuv_asn_filepath)
fuv_x1d_header = fits.getheader(fuv_x1d_filepath)
fuv_asn_header = fits.getheader(fuv_asn_filepath)
# This is the primary, 0th header of the calibrated nuv spectrum;
fuv_x1d_header[:18], "...", fuv_x1d_header[45:50]
# This is *not* the whole header...
# ...The [:18] and [45:50] tell Python to print the first 18 lines, as well as lines 45-50
For instance, we notice that the FUV data was taken in TIME-TAG mode and calibrated with CalCOS version 3.3.10 (at the time of writing this sentence - it may have been reprocessed by the time you read this).
However, some metadata information, such as the time of observation and calculated exposure time, can be found in the 1-th header rather than the 0th. We will read and print this below:
with fits.open(fuv_x1d_filepath) as hdu:
fuv_x1d_header1 = hdu[1].header
fuv_date = fuv_x1d_header1['DATE-OBS']
fuv_time = fuv_x1d_header1['TIME-OBS']
fuv_exptime = fuv_x1d_header1['EXPTIME']
# It's also perfectly valid to access the 1-th extension header using 'fits.getheader(fuv_x1d_filepath, ext=1)'
print(
f"This FUV data was taken on {fuv_date} starting at {fuv_time} with a net exposure time of {fuv_exptime} seconds.")
with fits.open(nuv_x1d_filepath) as hdu:
nuv_x1d_header1 = hdu[1].header
nuv_date = nuv_x1d_header1['DATE-OBS']
nuv_time = nuv_x1d_header1['TIME-OBS']
nuv_exptime = nuv_x1d_header1['EXPTIME']
print(
f"This NUV data was taken on {nuv_date} starting at {nuv_time} with a net exposure time of {nuv_exptime} seconds.")
1.2. Reading in the x1d/x1dsum Main Data¶
The data are in the 1-th header-data unit (HDU) of our fits file. There are several ways to read in our data from the our table-formatted fits file. We'll demonstrate three common methods below, focusing in on the astropy.table method.
We will then display all the fields contained in this data table using the .colnames method. You can ignore the warnings about multiple slashes in the units that come up while reading in the data. The proper units are displayed in LaTex as:
- 'erg /s /cm**2 /angstrom' ==> $$\ \ erg\ s^{-1}\ cm^{-2}\ \mathring{A}^{-1}$$
- 'count /s /pixel' ==> $$\ \ counts\ s^{-1}\ pixel^{-1}$$
The columns of these tables include some scalar values which describe the data (i.e. EXPTIME), while the columns containing actual data hold it in arrays of equal length (i.e. WAVELENGTH, FLUX, etc., where that length = NELEM).
# Method number 1:
with fits.open(fuv_x1d_filepath) as hdulist:
fuv_x1d_data = hdulist[1].data
print(f"Method 1 gets data as type: {type(fuv_x1d_data)}")
# Method number 2:
fuv_x1d_data = fits.getdata(fuv_x1d_filepath)
print(f"Method 2 gets data as type: {type(fuv_x1d_data)}")
# Method number 3:
fuv_x1d_data = Table.read(fuv_x1d_filepath)
print(f"Method 3 gets data as type: {type(fuv_x1d_data)}")
# We can easily explore this astropy table
columns = fuv_x1d_data.colnames
# Print basic info about the table's columns
print("\nTable of FUV data with columns:\n", columns, "\n")
# Display a representation of the data table:
fuv_x1d_data
In the case of the FUV data, we see an astropy style table of 2 rows which are labeled FUVA and FUVB. These rows contain data from the 2 segments of FUV Detector (see figure 1.1).
Fig. 1.1 from COS DHB Fig. 1.6¶
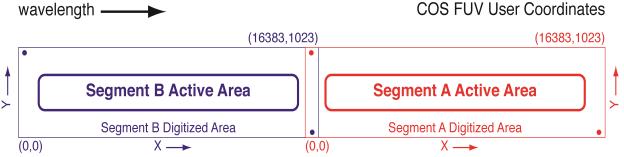
In the case of the NUV data, we see a similar astropy style table of 3 rows (labeled NUVA, NUVB, and NUVC). These rows contain data from the 3 stripes of the NUV spectrum (see figure 1.2).
Fig. 1.2 from COS DHB Fig. 1.10¶
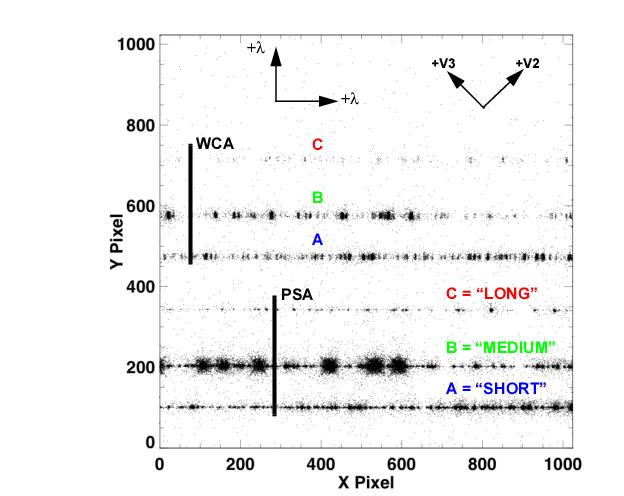
An important thing to note about this NUV data in particular is that with the grating used here (G230L), stripe C is actually a 2nd order spectrum with a higher dispersion and ~5% contamination from the 1st order spectrum. See the COS Data Handbook, especially Fig. 1.3, for more information.
1.3. The Association (asn) file¶
It's also likely we will want to see what observations went into making this calibrated spectrum. This information is contained in the Association (asn) file, under the MEMNAME column.
print(fits.info(fuv_asn_filepath), '\n\n----\n')
fuv_asn_data = Table.read(fuv_asn_filepath)
print(fuv_asn_data)
We see that our data has MEMTYPE = PROD-FP, meaning it is an output science product (see COS DHB Table 2.6.)
This particular association file lists four EXP-FP (input science exposure), with the MEMNAME values (Dataset IDs) [LCXV13FLQ, LCXV13FXQ, LCXV13G4Q, LCXV13GXQ]. We could look for these datasets, if we wished to inspect the exposures individually.
Exercise 1.1. Finding Metadata for the NUV¶
- Read in the NUV data, just as we did with the FUV data.
- From the 0th header of the
x1dsumfile, determine the time (in MJDs) that the data was processed. (keyword = PROCTIME) and from the 1th header, determine how many wavelength calibration "flashes" were used (keyword = NUMFLASH) - From the
asnfile, determine how many input science exposures went into the NUV x1dsum file.
# Your code here
2. Plotting the Data¶
2.1. Plotting an FUV Spectrum¶
Let's select the simplest data we need to plot a spectrum: WAVELENGTH, FLUX, and ERROR.
- Note that here, ERROR is flux error, which is discussed in the COS Instrument Handbook
- Also note that somewhat counterintuitively, the FUVB segment extends over shorter wavelengths than the FUVA.
2.1.1. Our First Plot¶
We begin with a simple plot: simply a line plot of a single segment (FUVA) without its error.
The goal of this show is to demonstrate some of the common parameters of making a simple plot with matplotlib which you are likely to often need. The comments explain what each line does.
# [0] Access FUVA data, the longer wvln segment and gets the data we need to plot a spectrum:
wvln, flux, segment = fuv_x1d_data[0]["WAVELENGTH", "FLUX", "SEGMENT"]
# Set up the plot as a single box with size of 10x4 inches, and with a dpi of 100, relevant should we choose to save it:
fig1, ax = plt.subplots(1, 1, figsize=(10, 4), dpi=100)
# The next few lines are the core of the cell, where we actually place the data onto the plot:
###############
ax.plot(wvln, flux, # First two arguments are assumed to be the x-data, y-data
# These parameters specify the look of the connecting line
linestyle="-", linewidth=0.25, c='black',
# The marker parameters specify how the data points will look...
marker='.', markersize=2, markerfacecolor='r', markeredgewidth=0,
# ... if you don't want dots set marker=''
label=segment) # The label is an optional parameter which will allow us to create a legend
# this label is useful when there are multiple datasets on the same plot
# The lines after this are all about formatting, adding text, and saving as an image
###############
ax.set_title("Fig. 2.1\nSimple COS Segment FUVA Spectrum",
size=20) # Adds a title of fontsize 20 points
ax.set_xlabel('Wavelength [$\AA$]', size=12) # Adds x axis label
# Adds y label
ax.set_ylabel('Flux [$erg\ s^{-1}\ cm^{-2}\ Angstrom^{-1}$]', size=12)
# These two lines set the x and y bounds of the image in whatever units we are plotting in
plt.xlim(1605, 1815)
plt.ylim(-1E-15, 1.85E-14)
# Adds a legend with the label specified in the plotting call
plt.legend(loc='upper right')
plt.tight_layout() # Trims blank space
# Optionally you can save the plot as an image
plt.savefig(str(plotsdir / "Fig2.1.png"))
plt.show() # Shows all the plot calls in this cell and "clears" the plotting space. Must come after any saving you want to do
Exercise 2.1: A clearer plot¶
Plot the data from Segment FUVB, similar to the Segment FUVA plot above, but this time, normalize flux to a max of 1, and don't plot the red markers, which can be distracting.
Note what can you simply copy over, and what you have to make sure to change.
# Your code here
2.1.2. A Complex Look at the Entire FUV¶
Now that we have an idea for how matplotlib works, let's make a more complicated graph showing both FUV segments - independently and together.
One of the most important steps to creating a plot is planning out how it will look and convey its information. We'll begin by planning this out below:
| Panel | Contents | Information Conveyed | Notes |
|---|---|---|---|
| top | Entire FUV Spectrum as a simple plot | Overview of the entire spectrum we have, coarse look without much detail | Color by segment |
| middle | Shorter Wavelength FUVB Spectrum as an errorbar plot | Closer look at the shorter wavelength spectrum with an idea of error | Color errorbar by segment, central line in black |
| bottom | Longer Wavelength FUVA Spectrum as an errorbar plot | Closer look at the longer wavelength spectrum with an idea of error | Color errorbar by segment, central line in black |
# ax0, ax1, ax2 are our 3 vertically-aligned panels: top, middle, and bottom
fig, (ax0, ax1, ax2) = plt.subplots(3, 1, figsize=(10, 10))
# Repeats for i=[0,1] to apply to each segment's data at a time
for i in range(2):
# Selects all useful data for the chosen segment
wvln, flux, fluxErr, segment = fuv_x1d_data[i]["WAVELENGTH",
"FLUX", "ERROR", "SEGMENT"]
# This section applies the top (0th) panel's plotting and formatting:
ax0.plot(wvln, flux,
linestyle="-", label=segment, c=segment_colors[segment])
ax0.legend(fontsize=20, loc='upper left')
ax0.set_title("Fig 2.2\nFUV Spectra with G160M Grating", size=35)
ax0.set_xlim(1428, 1805)
ax0.set_ylim(-1E-15, 1.9E-14)
######
if i == 0: # This indented code applies only to segment FUVA data in bottom Panel
markers, caps, bars = ax2.errorbar(x=wvln, y=flux, yerr=fluxErr,
linestyle="-", label=segment, marker='', markersize=1,
c='k', alpha=1, ecolor=segment_colors[segment])
ax2.set_xlim(1610, 1810)
ax2.set_ylim(-3E-15, 1.9E-14)
ax2.legend(fontsize=20, loc='upper left')
ax2.set_xlabel('Wavelength [$\AA$]', size=20)
[bar.set_alpha(0.75) for bar in bars]
######
if i == 1: # This indented code applies only to segment FUVB data in middle Panel
markers, caps, bars = ax1.errorbar(x=wvln, y=flux, yerr=fluxErr,
linestyle="-", label=segment, c='k', ecolor=segment_colors[segment])
ax1.set_xlim(1428, 1615)
ax1.set_ylim(-1E-15, 1.25E-14)
ax1.legend(fontsize=20, loc='upper left')
ax1.set_ylabel('Flux [$erg\ s^{-1}\ cm^{-2}\ Angstrom^{-1}$]', size=20)
[bar.set_alpha(0.75) for bar in bars]
######
plt.tight_layout()
plt.savefig(str(plotsdir / 'Fig2.2.png'), dpi=200)
plt.show()
2.1.3. Looking Closer at Parts of the FUV Spectrum¶
It can be very difficult to get any insights on small-scale details in the above plots because data is too dense to parse at once. Below, we'll show examples of:
- Plotting a small region around an absorption line feature.
- Plotting an entire segment's spectrum in segments of wavelength space.
Let's begin with showing a region around a line, in this case, we see a sharp line around 1670 Å.
line1670 = 1670.67 # By-eye center of the line for plotting
# Selects all useful data for the chosen segment
wvln, flux, fluxErr, segment = fuv_x1d_data[0]["WAVELENGTH",
"FLUX", "ERROR", "SEGMENT"]
wvln_extent = 2 # How many Angstroms in each direction around line1670 do we want to look at?
# Mask the data to within +/- wvln_extent Angstrom of the line - speeds up the plotting
lineRegion_mask = (wvln > line1670 - wvln_extent) & (wvln <
line1670 + wvln_extent)
# applies the created mask
wvln_region, flux_region, fluxErr_region = wvln[
lineRegion_mask], flux[lineRegion_mask], fluxErr[lineRegion_mask]
plt.figure(figsize=(8, 6)) # how big should the plot be
plt.axvline(x=line1670, c='k', linewidth=4, linestyle='dotted', # vertical line at x position line1670; color = 'k' AKA black, line thickness = 4 points, type of line is dotted
alpha=0.8, label="$Approximate\ line\ center$") # alpha sets transparency where 1 is opaque; label for the legend
plt.errorbar(x=wvln_region, y=flux_region, yerr=fluxErr_region, label='COS FUVA',
linestyle='', marker='.') # marker tells the point to look like a dot
plt.xlabel('Wavelength [$\AA$]', size=20)
plt.ylabel('Flux [$erg\ s^{-1}\ cm^{-2}\ Angstrom^{-1}$]', size=20)
plt.legend(fontsize=15)
plt.tight_layout()
plt.savefig(str(plotsdir / 'Fig2.3.png'), dpi=200)
plt.title("Fig. 2.3\nZoom in on the line at 1670 $\AA$", size=25)
The source we're looking at - the quasar 3C48 has a substantial redshift: $$z \approx 0.37$$
Source: Simbad search for 3C48
With that redshift, we can determine the rest-frame wavelength.
$$z = \dfrac{\lambda_{obs}-\lambda_{rest}}{\lambda_{rest}} \ \ \rightarrow\ \ \ \lambda_{rest} = \dfrac{\lambda_{obs}}{1+z}$$At that redshift, we see this line to be $\approx 1219$ Å. This is close to, and may correspond to, the Lyman-$\alpha$ transition.
Now we will create a much more complex plot, allowing us to visualize an entire segment's spectrum in fine detail
We'll split the spectrum into "segments" of ~10 Angstroms, and plot these segments in a vertical series. These plots may take a minute to create. If you want them to run quicker, hit the Interrupt the Kernel square-shaped button to stop the current cell from running (you will get an error message), and run this cell with a smaller number of rows.
%%time
# Let's see how long it takes with the above "Cell magic" ...
# (Cell magic is a Jupyter/iPython series of utilities: https://ipython.readthedocs.io/en/stable/interactive/magics.html)
for segment_row in fuv_x1d_data: # Apply the following to each segment's data at a time
# Selects all immediately useful data for the chosen segment
wvln, flux, fluxErr, segment = segment_row["WAVELENGTH",
"FLUX", "ERROR", "SEGMENT"]
minx, maxx = min(wvln), max(wvln)
miny, maxy = min(flux), max(flux)
rangex = maxx - minx
fig = plt.figure(figsize=(14, 20))
nRows = 15 # How many segments we wish to split the spectrum into
for i in range(nRows):
min_ = minx + i*rangex/nRows
max_ = minx + (i+1)*rangex/nRows
ax = plt.subplot(nRows, 1, i+1)
if i == 0: # A way to set Title, xlabel, and ylabel that will work independent of number of rows
ax.set_title(
f"Fig. 2.4{segment[-1]} \nSegment {segment} Spectrum split into segments", size=30)
if i == nRows - 1:
ax.set_xlabel("Wavelength [$\AA$]", size=30)
if i == int(nRows/2):
ax.set_ylabel(
'Flux [$erg\ s^{-1}\ cm^{-2}\ Angstrom^{-1}$]', size=30)
# Create the plot itself
ax.errorbar(wvln, flux, fluxErr, c=plt.cm.rainbow((i+1)/nRows), alpha=0.8,
marker='.', markerfacecolor='k', markersize=2, mew=0)
ax.set_xlim(min_, max_)
plt.tight_layout()
plt.savefig(
str(plotsdir / f'Fig2.4{segment[-1]}_{nRows}Rows_seg{segment}.png'), dpi=200)
plt.show()
print("\n----\n")
Exercise 2.2 Choosing and plotting a useful data range¶
That last plot was very dense with information. As practice plotting, make a scaled down version from just 1635 - 1675 Angstroms, and plot the data as a simple line graph.
# Your code here
2.1.4. Reading and plotting the data with specutils (OPTIONAL)¶
Note, this section is entirely optional, and simply meant to give you more options for how to plot a spectrum.
An alternative way to read in and work with spectral data is with the specutils package, which contains quite a bit of functionality for working with spectra. It also can make dealing with units easier, as it generally works well with astropy units and other modules. Make sure that your package is up to date (version $\ge$ 1.1). We describe installing specutils in our Notebook on setting up an environment.
specutils treats spectra as special python objects rather than lists, and reads in the entire spectrum over both segments.
Below is a simple example of using specutils to read-in, plot, and continuum-normalize our entire spectrum.
import specutils
from specutils.fitting import fit_generic_continuum
from matplotlib import rcParams
# The default fontsize it will use does not be clear at this plot size
rcParams.update({'font.size': 20})
spec1d = specutils.Spectrum1D.read(fuv_x1d_filepath)
fig, (ax0, ax1) = plt.subplots(2, 1, figsize=(10, 8))
# Plot the non-normalized flux
ax0.plot(spec1d.spectral_axis, spec1d.flux)
ax0.set_title(
"Fig. 2.5\nProducing spectra with specutils\nUn-normalized flux", size=20)
# Continuum Normalize the flux:
cont_norm_spec1d = spec1d / fit_generic_continuum(spec1d)(spec1d.spectral_axis)
# Plot the normalized flux
ax1.plot(cont_norm_spec1d.spectral_axis, cont_norm_spec1d.flux)
ax1.set_title("Normalized flux", size=20)
ax1.set_ylabel("Unitless")
plt.tight_layout()
plt.savefig(str(plotsdir / 'Fig2.5.png'), dpi=200)
plt.show()
# Not necessary for this plot, but gives us all the data separately
wvln, flux, fluxErr = spec1d.wavelength, spec1d.flux, spec1d.uncertainty.quantity
rcParams.update({'font.size': 10}) # Restore default fontsize
specutils also works with the visualization package Jdaviz.Specviz, to produce very useful interactive spectral plots within a jupyter Notebook GUI framework. Currently, this interactive program works well within the Jupyter Notebook environment, but not within Jupyter Lab environment.
# Here we read in the data - we may ignore warnings about slashes in the notation
nuv_x1d_data = Table.read(nuv_x1d_filepath)
2.2.1. Examining the first-order spectrum¶
Again, let's select the simplest data we need to plot a spectrum: WAVELENGTH, FLUX, and ERROR.
We will limit this first plot to only our first order spectra (we will exclude stripe C). We will plot these two spectra together (in the top panel) and then stripe-by-stripe in the lower 2 panes, similar to fig. 2.2.
- The former view gives a better sense of the continuum
- The latter views show zooms which allow us to meaningfully view the errors and see specific emission/absorption features.
The way we produce this plot with Python in the cell below is looping through both NUV first-order stripes - NUVA and NUVB - plotting both of them in the upper subplot, and plotting each of them once more in one of the lower two subplots.
# Build a 3row x 1column - subplot figure
fig, (ax0, ax1, ax2) = plt.subplots(3, 1, figsize=(16, 16))
for i in range(2): # Iterate through the first 2 NUV segments/stripes
wvln, flux, fluxErr, segment = nuv_x1d_data[i]["WAVELENGTH"], nuv_x1d_data[i]["FLUX"], \
nuv_x1d_data[i]["ERROR"], nuv_x1d_data[i]["SEGMENT"] # Gather data
ax0.plot(wvln, flux, # Plot both segments/stripes in first panel
linestyle="-", label=segment, c=segment_colors[segment])
ax0.legend(fontsize=20)
ax0.set_title(
"Fig 2.6\nFirst-order NUV Spectra with G230L Grating", size=35)
if i == 0: # Plot only 0th segment/stripe in 2nd panel
ax1.errorbar(x=wvln, y=flux, yerr=fluxErr,
linestyle="", label=segment, c=segment_colors[segment])
ax1.set_xlim(2100, 2510)
ax1.set_ylim(0.5E-13, 1.5E-13)
ax1.legend(fontsize=20)
ax1.set_ylabel('Flux [$erg\ s^{-1}\ cm^{-2}\ Angstrom^{-1}$]', size=30)
if i == 1: # Plot only 1th segment/stripe in 3rd panel
ax2.errorbar(x=wvln, y=flux, yerr=fluxErr,
linestyle="", label=segment, c=segment_colors[segment])
ax2.set_xlim(3190, 3600)
ax2.set_ylim(1E-14, 4.5E-14)
ax2.legend(fontsize=20)
ax2.set_xlabel('Wavelength [$\AA$]', size=30)
plt.tight_layout()
plt.savefig(str(plotsdir / 'Fig2.6.png'), dpi=200)
plt.show()
2.2.2. Examining the second-order spectrum¶
On NUV stripe C data taken with the grating G230L, we have a more dispersed, second-order spectrum over a smaller segment of the NUV. Below, we plot this second-order over the first-order spectrum from stripe A.
Note that most NUV gratings produce first-order spectra over all three stripes. See the Instrument Handbook for more information. We chose to plot this this type of spectrum to create a more complex plot and to demonstrate using different scales on the same axis.
fig, (ax0, ax1) = plt.subplots(2, 1, figsize=(16, 8))
# We reverse this order. The 0th stripe (A) is plotted OVER the 2nd stripe (C). It's purely aesthetic.
for i in [2, 0]:
wvln, flux, fluxErr, segment = nuv_x1d_data[i]["WAVELENGTH"], nuv_x1d_data[
i]["FLUX"], nuv_x1d_data[i]["ERROR"], nuv_x1d_data[i]["SEGMENT"]
if i == 0:
ax0.errorbar(x=wvln, y=flux, yerr=fluxErr,
linestyle="", label=segment, c='k', alpha=0.3)
ax1.errorbar(x=wvln, y=flux, yerr=fluxErr,
linestyle="", label=segment, c='k', alpha=0.3)
if i == 2:
ax0.errorbar(x=wvln, y=flux, yerr=fluxErr,
linestyle="", label=segment, c=segment_colors[segment], alpha=0.8)
ax1.errorbar(x=wvln, y=flux, yerr=fluxErr,
linestyle="", label=segment, c=segment_colors[segment], alpha=0.8)
ax0.set_xlim(2100, 2510)
ax0.set_ylim(0.48E-13, 1.75E-13)
ax0.set_title(
"Fig 2.7\nOverlay of First and Second-order Spectrum with G230L Grating", size=25)
ax1.set_xlim(2200, 2210)
ax1.set_ylim(0.6E-13, 1.75E-13)
ax1.set_xlabel('Wavelength [$\AA$]', size=20)
fig.text(-0.015, 0.5, 'Flux [$erg\ s^{-1}\ cm^{-2}\ Angstrom^{-1}$]',
size=20, va='center', rotation='vertical')
# Let's add a dashed rectangle to show where we are zooming into in the lower panel.
ax0.plot([2210, 2200, 2200, 2210, 2210], [0.6E-13, 0.6E-13, 1.7E-13, 1.7E-13, 0.6E-13],
'b', linewidth=5, linestyle='--', alpha=0.7, label="Lower panel zoom bounds")
# These lines just ensure that the legend is ordered correctly (first ax0)
handles, labels = ax0.get_legend_handles_labels()
handles = [handles[2], handles[1], handles[0]]
labels = [labels[2], labels[1], labels[0]]
ax0.legend(handles, labels, fontsize=20, loc='upper right')
handles, labels = ax1.get_legend_handles_labels() # Now for ax1
handles = [handles[1], handles[0]]
labels = [labels[1], labels[0]]
ax1.legend(handles, labels, fontsize=20, loc='upper right')
plt.tight_layout()
plt.savefig(str(plotsdir / 'Fig2.7.png'), dpi=200)
plt.show()
Clearly, our errorbars on the second-order spectrum are much larger.
However, if we need a very high dispersion - for instance, to split closely-spaced lines - the lower panel (zoom) shows a potential advantage of stripe C. Its higher spectral sampling rate can allow for finer distinctions in wavelength, if an acceptable SNR can be reached.
3. Preliminary Review of the Data¶
There is no one-size-fits-all approach to analyzing COS data.
This section aims to walk you through taking a brief critical look at your data by taking the first steps of binning the data, (to the size of COS' resolution elements - called resels), and then measuring the Signal-to-Noise Ratio (SNR).
Note that the cell below is only necessary if you have chosen to skip sections #1 and #2
# Make sure these point to your new FUV data
fuv_x1d_filepath = './data/mastDownload/HST/lcxv13050/lcxv13050_x1dsum.fits'
fuv_x1d_data = Table.read(fuv_x1d_filepath)
# Make sure these point to your new NUV data
nuv_x1d_filepath = './data/mastDownload/HST/lbbd01020/lbbd01020_x1dsum.fits'
nuv_x1d_data = Table.read(nuv_x1d_filepath)
3.1. Data Quality and Initial Cleanup¶
One of the first things one notices in all of the plots we have made is that all of the segments/stripes have real, useful data, bookended on each side by zeros (see, for example, Fig. 2.1). These zeros are regions on the active area of the detector which don't receive and detect light, but are read in as data. We don't want these datapoints in our spectra, so we will filter them out.
The COS data we have downloaded conveniently have an extension devoted to data quality information. Information on the data quality array and the flags it contains can be found in Table 2.18 of the COS Data Handbook.
Let's first look at the data quality flags. We'll do this by plotting a histogram, labelling the bins according to what the data quality value of that bin means. We add hatching to the histograms to make it easier to see where certain segments overlap.
# To make plotting the bins linearly work, we deal with the base2 logs of the power-of-2 data quality values
# The values are all powers of two from 2**1 to 2**14, except for 0, which is 2**-inf
bins_titles = (np.logspace(-1, 14, 16, base=2, dtype=int))
meanings = ['No Anomalies', 'Reed-Solomon Error', 'Hot Spot', 'Detector Shadow', 'Poorly Calibrated Region', # What each power of 2 means in order
# More info in the data handbook
'Very-low Response Region', 'Background Feature', 'Burst', 'Pixel Out-of-bounds', 'Fill Data',
'Pulse Height Out-of-bounds', 'Low Response Region', 'Bad Time Interval', 'Low PHA Feature',
'Gain-sag Hole', 'Not Used']
# pair the meaning with its power of 2 value in a single string
meanings2 = [str(bt)+": " + mn for bt, mn in zip(bins_titles, meanings)]
# Top (FUV) subplot and bottom (NUV) subplot
fig, (ax0, ax1) = plt.subplots(2, 1, figsize=(10, 12))
# Suppress a divide by zero warning
np.warnings.filterwarnings('ignore', category=RuntimeWarning)
for i in range(2): # First loop through the 2 FUV segments to make the top plot
# Gather the data
dataQual, segment = fuv_x1d_data[i]["DQ"], fuv_x1d_data[i]["SEGMENT"]
bins_ = np.arange(-1, 15) # all the log2 of the DQ values
bins_titles = (np.logspace(-1, 14, 16, base=2, dtype=int))
logDQ = np.log2(dataQual)
logDQ = np.nan_to_num(logDQ, neginf=-1)
ax0.set_xticks([])
# Add hatching to distinguish overlapping colors
ax0.hist(logDQ, bins=bins_, color='cmy'[
i], alpha=0.5 + 0.1*(i+1), label=segment, hatch='|-'[i])
ax0.legend(fontsize=20)
ax0.set_yscale('log')
ax0.set_title("Fig. 3.1\nData quality flag frequencies", fontsize=20)
for i in range(3): # Next loop through the 3 NUV segments/stripes to make bottom plot
# Gather the data
dataQual, segment = nuv_x1d_data[i]["DQ"], nuv_x1d_data[i]["SEGMENT"]
bins_ = np.arange(-1, 15) # all the log2 of the DQ values
logDQ = np.log2(dataQual)
logDQ[np.where(-1*(logDQ) == np.inf)] = -1
# Add hatching to distinguish overlapping colors
ax1.hist(logDQ, bins=bins_, color='cmy'[
i], alpha=1 - 0.25*(i), label=segment, hatch='|-/'[i])
ax1.legend(fontsize=20)
ax1.set_yscale('log')
# suppress a divide by zero warning
np.warnings.filterwarnings('default', category=RuntimeWarning)
plt.xticks(bins_+0.5, labels=meanings2, rotation='vertical', fontsize=15)
fig.set_tight_layout('tight')
plt.savefig(str(plotsdir / 'Fig3.1.png'), dpi=200)
When the data is processed through CalCOS, it has a summed set of "Serious Data Quality" SDQ flags attached to it in the form of a single integer between 0 and $2^{15}$. This value is found in the 1-th header as "SDQFLAGS". This can be decomposed into the powers of 2 data flags above, (by showing its binary representation,) and tells the pipeline whether to weight that pixel in that exposure by 0 or 1. These weights are then stored in the x1d and x1dsum files, in the "DQ_WGT" column. The "DQ_WGT" value for a given pixel in the x1dsum file will then be equal to the number of exposures which went into creating that x1dsum file in which no serious data quality flags apply to that pixel.
Below, we first see which data quality flags the pipeline considered "serious", and then demonstrate masking out the datapoints assigned a weight of 0.
sdqFlags_fuv = fits.getheader(fuv_x1d_filepath, 1)["SDQFLAGS"]
print(
f"The FUV was processed with SDQFLAGS = {sdqFlags_fuv}, which in binary is {bin(sdqFlags_fuv)[2:]}")
print("\t\tThus, the following DQ-flagged data get weighted by 0:\n")
for i, char in enumerate(bin(sdqFlags_fuv)[2:]):
if char == '1':
print(f"\t\t\t{(2**(i+1))}'s place - ", meanings[i+2])
# Filter the datapoints to where there are no serious DQ flags
mask_noSDQ = fuv_x1d_data[0]["DQ_WGT"].astype(bool)
wvln_FUVA_noSDQ, flux_FUVA_noSDQ = fuv_x1d_data[0]["WAVELENGTH"][
mask_noSDQ], fuv_x1d_data[0]["FLUX"][mask_noSDQ]
# Make the figure:
plt.figure(figsize=(10, 6))
# Plot the filtered datapoints
plt.plot(wvln_FUVA_noSDQ, flux_FUVA_noSDQ)
# Format the figure
plt.title("Fig 3.2\nFUVA without SDQ flagged data", size=20)
plt.xlabel('Wavelength [$\AA$]', size=20)
plt.ylabel('Flux [$erg\ s^{-1}\ cm^{-2}\ Angstrom^{-1}$]', size=15)
plt.tight_layout()
plt.savefig(str(plotsdir / 'Fig3.2.png'), dpi=200)
Alternatively, we can ignore the SDQFLAGS and the weights decided by CalCOS and pick which data quality flags we want to filter out. From Fig 3.1, we know the only problem in the FUV and the largest problem in the NUV are pixels flagged by "out of bounds", corresponding to Data Quality: 128.
We will demonstrate removing only these datapoints from the FUV data below. You could also filter to only data with 0: no anomalies, or to any other subset.
plt.figure(figsize=(12, 6), dpi=100)
for i in range(2):
wvln, flux, fluxErr, dataQual, segment = fuv_x1d_data[i]["WAVELENGTH"], fuv_x1d_data[i]["FLUX"],\
fuv_x1d_data[i]["ERROR"], fuv_x1d_data[i]["DQ"], fuv_x1d_data[i]["SEGMENT"]
plt.plot(wvln[dataQual != 128.0], flux[dataQual != 128.0], linewidth=1, alpha=0.8, c=['#d55e00', '#009e73'][i],
label=f"{segment} Cleaned")
plt.scatter(wvln[dataQual == 128.0], flux[dataQual == 128.0],
s=[12, 4][i], c=['k', 'b'][i], alpha=1, marker="o."[i],
label=f"{segment} Pix out-of-bounds")
plt.legend(fontsize=18)
plt.title("Fig. 3.3\nRemoving only out-of-bounds pixels from the FUV\n", size=25)
plt.xlabel('Wavelength [$\AA$]', size=20)
plt.ylabel('Flux [$erg\ s^{-1}\ cm^{-2}\ Angstrom^{-1}$]', size=15)
plt.tight_layout()
plt.savefig(str(plotsdir / 'Fig3.3.png'))
Exercise 3.1: Removing all flagged data from the NUV¶
The NUV data has flags for more than just out-of-bounds pixels.
- Filter out all data which has been flagged
- Plot the NUV spectrum from stripes NUVA and NUVB
- Plot the flagged data in another color to see where the removed data is
# Your answer here
3.2. Binning¶
Up until now, the data we've been working with has one value per "pixel" of the detector. COS data is generally binned to a resolution element, or resel, when working with it. These resels are generally the following sizes in pixels.
| FUV | NUV | |
|---|---|---|
| Dispersion Axis | 6 | 3 |
| Cross-Dispersion Axis | 10 | 3 |
So, for the FUV, we generally want to preliminarily bin our x1d or x1dsum data by 6.
3.2.1. Bringing in Some Useful Functions for Binning¶
In the same subdirectory of the spacetelescope/notebooks GitHub repository as this file (notebooks/COS/ViewData/), we also have the Python file: cos_functions.py, in which we have defined several long functions necessary for this data processing.
Note, if you downloaded this Notebook file without cloning the entire GitHub repository, you must also download the file cos_functions.py from here.
In the cell below, we import the function bin_by_resel from the file cos_functions.py. The bin_by_resel function applies the following binning algorithms to an entire COS NUV or FUV dataset. We run the help function to get more information on how the values are binned.
from cos_functions import bin_by_resel
help(bin_by_resel)
3.2.2. Binning the FUV Data¶
Below we bin our FUV data by 6. Our resulting table is just under $\dfrac{1}{6}$ the size of our input table, as a few of the last datapoints were cropped.
Note, this binning method works well for binsizes which are small compared to the spectrum; however, if you increase your binsize significantly, you may lose important datapoints.
binned_fuv_data = bin_by_resel(fuv_x1d_data)
print(f"\nOriginal Dataset Length is {len(fuv_x1d_data[0]['WAVELENGTH'])}")
print(f"Binned Dataset Length is {len(binned_fuv_data[0]['WAVELENGTH'])}")
print(f"\t{len(fuv_x1d_data[0]['WAVELENGTH'])} over {len(binned_fuv_data[0]['WAVELENGTH'])} = {len(fuv_x1d_data[0]['WAVELENGTH'])/len(binned_fuv_data[0]['WAVELENGTH'])}\n")
binned_fuv_data
3.3. Estimating the Signal-to-Noise (SNR) Ratio¶
3.3.1. Bringing in a Useful Function for Estimating SNR¶
Below, we define a function to estimate the Signal-to-Noise ratio (SNR or S/N) of our data. One way to estimate the SNR for photon-counting instruments like COS is by the square-root of their number of gross counts. This is a simplification of the equation given for point sources in the COS Instrument Handbook Section 7.3:
$$\dfrac{Signal}{Noise} = \dfrac{C \times t}{\sqrt{C \times t + N_{pix} \times (B_{sky} + B_{det}) \times t}}$$For bright point sources, $C >> B_{sky} + B_{det}$, and this approaches the simpler:
$$\dfrac{Signal}{Noise} = \sqrt{C \times t} = \sqrt{Gross\ Counts}$$Caution!
 This simplification may not hold very well if your source is diffuse or faint.
This simplification may not hold very well if your source is diffuse or faint.
from cos_functions import estimate_snr
help(estimate_snr)
The function estimate_snr gives a $\sqrt{Gross\ Counts}$ estimate of SNR for an input Astropy Table of COS data.
By default, it does not bin the data before calculating the SNR, nor does it weight the output SNR by exposure time; however, it has the functionality to do both. In most cases, a range should be specified over which to calculate the SNR. If no range is specified, then SNR will be computed for all Resels, but no mean/weighted average will be computed; instead, -1 will be returned in place of the mean.
3.3.2. Choosing a Region to calculate SNR¶
The SNR should be calculated over a region of continuum, rather than one with significant spectral lines. Looking back to Fig. 2.4, we see a broad stretch with no obvious lines from [1675 - 1690 Å] in the FUVA segment. We'll make a quick plot of that region below just to check.
plt.figure(figsize=(12, 4)) # Set up figure
wvln, flux = fuv_x1d_data[0]["WAVELENGTH", "FLUX"] # select data
wvln_range_mask = (wvln > 1670) & (wvln < 1700) # create mask for data
# Generate the plot itself
plt.plot(wvln[wvln_range_mask], flux[wvln_range_mask])
# add lines showing the range we'll calculate SNR over
plt.axvline(1675, c='k', linewidth=3)
plt.axvline(1690, c='k', linewidth=3)
# Format the plot
plt.title("Fig. 3.4\nRange for SNR Calculation", size=20)
plt.xlabel('Wavelength [$\AA$]', size=20)
plt.ylabel('Flux\n[$erg\ s^{-1}\ cm^{-2}\ Angstrom^{-1}$]', size=12)
plt.tight_layout()
plt.savefig(str(plotsdir/'Fig3.4.png'), dpi=200)
Our chosen region, between the black lines, looks quite good for calculating SNR, as it lacks obvious spectral lines.
3.3.3. Calculating the SNR¶
Below, we calculate the SNR of the FUV data over the region [1675, 1690]. Note, we input the unbinned data, and bin by an FUV Resel of 6 first. We'll leave verbose = True, so we can see what is going on in the function.
It turns out this dataset has a fairly low SNR. After calculating the SNR and mean SNR over the specified region, we plot both over wavelength.
# Calculates the SNR
res_size = 6 # Set the correct resel size as in the data handbook
meanSNR_range1675_1690, range1675_1690 = estimate_snr(
fuv_x1d_data, bin_data_first=True, binsize_=res_size, snr_range=[1675, 1690]) # Gather data
# Creates a plot
plt.figure(figsize=(12, 8))
wvln_over_range, snr_over_range = range1675_1690[0][0], range1675_1690[0][1]
# range1675_1690 contains a list of data for each segment of the detector (i.e. FUVA and FUVB)
# If your wavelength range for calculating S/N falls in FUVA, you would access the WAVELENGTH and S/N as:
# range1675_1690[1][0], range1675_1690[1][1]
plt.plot(wvln_over_range, snr_over_range, c='#466599',
# add a marker (black dot) to the plotted line
marker='.', markersize=8, markerfacecolor='k',
label=f"SNR Binned by Resel size {res_size}")
plt.axhline(meanSNR_range1675_1690, c='r', linestyle='-.', linewidth=4,
label="Mean SNR over the Region") # plot a horizontal line at y = mean SNR
plt.legend(fontsize=20)
plt.title("Fig. 3.5\nResults of SNR Calculation by Wavelength", size=30)
plt.xlabel('Wavelength [$\AA$]', size=20)
plt.ylabel('SNR', size=20)
plt.tight_layout()
plt.savefig(str(plotsdir/'Fig3.5.png'), dpi=200)
Exercise 3.2. Binning the NUV Data and Calculating its SNR¶
- Bin the NUV data, remembering that the resel size is different than that for the FUV
- Find a continuum region of the NUV data with no significant spectral lines
- Calculate the mean SNR over that region
# Your code here
About this Notebook¶
Author: Nat Kerman
Updated On: 2022-03-17
This tutorial was generated to be in compliance with the STScI style guides and would like to cite the Jupyter guide in particular.
Citations¶
If you use astropy, matplotlib, astroquery, or numpy for published research, please cite the
authors. Follow these links for more information about citations:
Exercise Solutions:¶
# Exercise 1.1 Soln
# 1
# Here we read in the data - we may ignore any warnings about slashes in the notation
nuv_x1d_data = Table.read(nuv_x1d_filepath)
# 2
nuv_x1d_header = fits.getheader(nuv_x1d_filepath)
nuv_x1d_header1 = fits.getheader(nuv_x1d_filepath, ext=1)
print(
f"Processed at MJD = {nuv_x1d_header['PROCTIME']}\nTaken with {nuv_x1d_header1['NUMFLASH']} wavecal flashes\n")
# 3
nuv_asn_data = Table.read(nuv_asn_filepath)
print(nuv_asn_data)
# Ex. 2.1 Soln:
# [0] Accesses FUVA: the longer wvln segment and gets the data we need to plot a spectrum
wvln, flux, segment = fuv_x1d_data[1]["WAVELENGTH", "FLUX", "SEGMENT"]
# [1] Accesses FUVB
wvln *= u.AA # Adds unit to the wvln of Angstroms
# Adds unit to the flux of erg / (Angstrom cm2 s)
flux *= u.erg/(u.second * u.AA * (u.cm)**2)
flux /= (np.nanmax(flux))
with quantity_support(): # Allows us to view the units attached to the data as the axes labels. This isn't generally necessary unless you want the unit support.
# Sets up the plot as a single box with size of 10x4 inches, and with a dpi of 100, relavent should we choose to save it
fig1, ax = plt.subplots(1, 1, figsize=(10, 4), dpi=100)
# The next few lines are the core of the cell, where we actually place the data onto the plot:
###############
ax.plot(wvln, flux, # First two arguments are assumed to be the x-data, y-data
# These parameters specify the look of the connecting line
linestyle="-", linewidth=0.25, c='black',
marker='', # The marker parameters specify how the data points will look - if you don't want dots set marker = ''
label=segment) # The label is an optional parameter which will allow us to create a legend - useful when there are multiple datasets on the same plot
ax.set_title("Exercise 2.1\nSimple COS Segment FUVB Spectrum",
size=20) # Adds a title of fontsize 20 points
# These two lines set the x and y bounds of the image in whatever units we are plotting in
plt.xlim(1420, 1620)
plt.ylim(-0.05, 1)
# Adds a legend with the label specified in the plotting call
plt.legend(loc='upper right')
plt.tight_layout() # Gets rid of blank space
plt.show() # Shows all the plot calls in this cell and "clears" the plotting space - must come after any saving you want to do
# Ex. 2.2 Soln
# selects all useful data for the chosen segment = FUVA
wvln, flux, fluxErr, segment = fuv_x1d_data[0]["WAVELENGTH",
"FLUX", "ERROR", "SEGMENT"]
minx, maxx = 1635, 1675
miny, maxy = min(flux), max(flux)
wvln_range_mask = (wvln > minx) & (wvln < maxx)
wvln = wvln[wvln_range_mask]
flux = flux[wvln_range_mask]
fluxErr = fluxErr[wvln_range_mask]
rangex = maxx - minx
fig = plt.figure(figsize=(14, 10))
nRows = 3
for i in range(nRows):
min_ = minx + i*rangex/nRows
max_ = minx + (i+1)*rangex/nRows
ax = plt.subplot(nRows, 1, i+1)
if i == 0: # A way to set Title, xlabel, and ylabel that will work independent of number of rows
ax.set_title(
f"Ex 2.2 Solution FUV{segment[-1]} \nSegment {segment} spectrum split into segments", size=30)
if i == nRows - 1:
ax.set_xlabel("Wavelength [$\AA$]", size=30)
if i == int(nRows/2):
ax.set_ylabel('Flux [$erg\ s^{-1}\ cm^{-2}\ Angstrom^{-1}$]', size=30)
ax.errorbar(wvln, flux, fluxErr, c=plt.cm.rainbow((i+1)/nRows), alpha=0.8,
marker='.', markerfacecolor='k', markersize=2, mew=0)
ax.set_xlim(min_, max_)
plt.tight_layout()
plt.show()
# Ex. 3.1 Soln
plt.figure(figsize=(12, 6))
for i in range(2):
dataQual = nuv_x1d_data[i]["DQ"]
wvln, flux, fluxErr, segment = nuv_x1d_data[i]["WAVELENGTH"], nuv_x1d_data[i]["FLUX"],\
nuv_x1d_data[i]["ERROR"], nuv_x1d_data[i]["SEGMENT"]
plt.plot(wvln[dataQual == 0], flux[dataQual == 0], linewidth=1, alpha=0.5,
label=f"{segment} Un-Flagged Pixel")
plt.scatter(wvln[dataQual != 0], flux[dataQual != 0], s=2, c='r', alpha=1,
label=f"{segment} Flagged Pixel")
plt.legend(fontsize=18)
plt.title(
"Ex 3.1 Solution\nRemoving only out-of-bounds pixels from the NUV\n", size=30)
plt.xlabel('Wavelength [$\AA$]', size=20)
plt.ylabel('Flux [$erg\ s^{-1}\ cm^{-2}\ Angstrom^{-1}$]', size=15)
plt.tight_layout()
# Ex. 3.2 Soln
# This whole process can be accomplished in one line, provided we use Fig 2.6 to find a line free region.
# We use the estimate_snr function to bin by the NUV resel size of 3, then mean calculate SNR over the region.
meanSNR_nuv_range, nuv_range = estimate_snr(
nuv_x1d_data, bin_data_first=True, binsize_=3, snr_range=[3400, 3450])
# Let's plot it as in Fig 3.5
plt.figure(figsize=(12, 8))
plt.plot(nuv_range[1][0], nuv_range[1][1], label="SNR Binned by Resel")
plt.axhline(meanSNR_nuv_range, c='r', linestyle='-.',
linewidth=4, label="Mean SNR over the Region")
plt.legend(fontsize=20)
plt.title("Ex. 3.2 Solution\nResults of SNR Calculation", size=30)
plt.xlabel('Wavelength [$\AA$]', size=20)
plt.ylabel('SNR', size=20)
plt.tight_layout()
