Hubble Catalog of Variables Notebook (API version)#
2019 - 2022, Rick White, Steve Lubow, Trenton McKinney#
This notebook shows how to access the Hubble Catalogs of Variables (HCV). The HCV is a large catalog of faint variable objects extracted from version 3 of the Hubble Source Catalog. The HCV project at the National Observatory of Athens was funded by the European Space Agency (PI: Alceste Bonanos). The data products for the HCV are available both at the ESA Hubble Archive at ESAC through the HCV Explorer interface and at STScI.
This notebook uses the MAST HSC catalog interface, which supports queries to the current and previous versions of the Hubble Source Catalog. It allows searches of several different tables including the HCV summary and detailed tables. It also has an associated API that is used for data access in this notebook.
For similar examples using the MAST CasJobs interface, a SQL database query interface that is more complex to use, but more powerful than the API, see HCV_CasJobs.
Instructions#
Complete the initialization steps described below.
Run the initialization steps before running the rest of the notebook.
Modify and rerun any sections of the Table of Contents below.
Table of Contents#
Initialization #
Install Python modules#
This notebook requires the use of Python 3.
Modules can be installed with
conda, if using the Anaconda distribution of python, or withpip.If you are using
conda, do not install / update / remove a module withpip, that exists in acondachannel.If a module is not available with
conda, then it’s okay to install it withpip
import astropy
from astropy.coordinates import SkyCoord
import time
import sys
import os
import requests
import json
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
from io import BytesIO
from astropy.table import Table, join
from astropy.io import ascii
# set width for pprint
astropy.conf.max_width = 150
# set universal matplotlib parameters
plt.rcParams.update({'font.size': 16})
MAST API functions#
Here we define several interrelated functions for retrieving information from the MAST API.
The
hcvcone(ra, dec, radius [, keywords])function searches the HCV catalog near a position.The
hcvsearch()function performs general non-positional queries.The
hcvmetadata()function gives information about the columns available in a table.
hscapiurl = "https://catalogs.mast.stsci.edu/api/v0.1/hsc"
def hcvcone(ra, dec, radius, table="hcvsummary", release="v3", format="csv", magtype="magaper2",
columns=None, baseurl=hscapiurl, verbose=False, **kw):
"""Do a cone search of the HSC catalog (including the HCV)
Parameters
----------
ra (float): (degrees) J2000 Right Ascension
dec (float): (degrees) J2000 Declination
radius (float): (degrees) Search radius (<= 0.5 degrees)
table (string): hcvsummary, hcv, summary, detailed, propermotions, or sourcepositions
release (string): v3 or v2
magtype (string): magaper2 or magauto (only applies to summary table)
format: csv, votable, json
columns: list of column names to include (None means use defaults)
baseurl: base URL for the request
verbose: print info about request
**kw: other parameters (e.g., 'numimages.gte':2)
"""
data = kw.copy()
data['ra'] = ra
data['dec'] = dec
data['radius'] = radius
return hcvsearch(table=table, release=release, format=format, magtype=magtype,
columns=columns, baseurl=baseurl, verbose=verbose, **data)
def hcvsearch(table="hcvsummary", release="v3", magtype="magaper2", format="csv",
columns=None, baseurl=hscapiurl, verbose=False, **kw):
"""Do a general search of the HSC catalog (possibly without ra/dec/radius)
Parameters
----------
table (string): hcvsummary, hcv, summary, detailed, propermotions, or sourcepositions
release (string): v3 or v2
magtype (string): magaper2 or magauto (only applies to summary table)
format: csv, votable, json
columns: list of column names to include (None means use defaults)
baseurl: base URL for the request
verbose: print info about request
**kw: other parameters (e.g., 'numimages.gte':2). Note this is required!
"""
data = kw.copy()
if not data:
raise ValueError("You must specify some parameters for search")
if format not in ("csv", "votable", "json"):
raise ValueError("Bad value for format")
url = f"{cat2url(table, release, magtype, baseurl=baseurl)}.{format}"
if columns:
# check that column values are legal
# create a dictionary to speed this up
dcols = {}
for col in hcvmetadata(table, release, magtype)['name']:
dcols[col.lower()] = 1
badcols = []
for col in columns:
if col.lower().strip() not in dcols:
badcols.append(col)
if badcols:
raise ValueError(f"Some columns not found in table: {', '.join(badcols)}")
# two different ways to specify a list of column values in the API
# data['columns'] = columns
data['columns'] = f"[{','.join(columns)}]"
# either get or post works
# r = requests.post(url, data=data)
r = requests.get(url, params=data)
if verbose:
print(r.url)
r.raise_for_status()
if format == "json":
return r.json()
else:
return r.text
def hcvmetadata(table="hcvsummary", release="v3", magtype="magaper2", baseurl=hscapiurl):
"""Return metadata for the specified catalog and table
Parameters
----------
table (string): hcvsummary, hcv, summary, detailed, propermotions, or sourcepositions
release (string): v3 or v2
magtype (string): magaper2 or magauto (only applies to summary table)
baseurl: base URL for the request
Returns an astropy table with columns name, type, description
"""
url = f"{cat2url(table,release,magtype,baseurl=baseurl)}/metadata"
r = requests.get(url)
r.raise_for_status()
v = r.json()
# convert to astropy table
tab = Table(rows=[(x['name'], x['type'], x['description']) for x in v],
names=('name', 'type', 'description'))
return tab
def cat2url(table="hcvsummary", release="v3", magtype="magaper2", baseurl=hscapiurl):
"""Return URL for the specified catalog and table
Parameters
----------
table (string): hcvsummary, hcv, summary, detailed, propermotions, or sourcepositions
release (string): v3 or v2
magtype (string): magaper2 or magauto (only applies to summary table)
baseurl: base URL for the request
Returns a string with the base URL for this request
"""
checklegal(table, release, magtype)
if table == "summary":
url = f"{baseurl}/{release}/{table}/{magtype}"
else:
url = f"{baseurl}/{release}/{table}"
return url
def checklegal(table, release, magtype):
"""Checks if this combination of table, release and magtype is acceptable
Raises a ValueError exception if there is problem
"""
releaselist = ("v2", "v3")
if release not in releaselist:
raise ValueError(f"Bad value for release (must be one of {', '.join(releaselist)})")
if release == "v2":
tablelist = ("summary", "detailed")
else:
tablelist = ("summary", "detailed", "propermotions", "sourcepositions", "hcvsummary", "hcv")
if table not in tablelist:
raise ValueError(f"Bad value for table (for {release} must be one of {', '.join(tablelist)})")
if table == "summary":
magtypelist = ("magaper2", "magauto")
if magtype not in magtypelist:
raise ValueError(f"Bad value for magtype (must be one of {', '.join(magtypelist)})")
Variable objects near IC 1613 #
Use MAST name resolver to get position of IC 1613 #
target = 'IC 1613'
coord_ic1613 = SkyCoord.from_name(target)
ra_ic1613 = coord_ic1613.ra.degree
dec_ic1613 = coord_ic1613.dec.degree
print(f'ra: {ra_ic1613}\ndec: {dec_ic1613}')
ra: 16.2016962
dec: 2.1194959
Select objects near IC 1613 from HCV #
This searches the HCV summary table for objects within 0.5 degrees of the galaxy center. Note that this returns both variable and non-variable objects.
radius = 0.5 # degrees
t0 = time.time()
tab = ascii.read(hcvcone(ra_ic1613, dec_ic1613, radius, table="hcvsummary"))
print("Completed in {:.1f} sec".format(time.time()-t0))
# clean up the output format
tab['MeanMag'].format = "{:.3f}"
tab['MeanCorrMag'].format = "{:.3f}"
tab['MAD'].format = "{:.4f}"
tab['Chi2'].format = "{:.4f}"
tab['RA'].format = "{:.6f}"
tab['Dec'].format = "{:.6f}"
# show some of the variable sources
tab[tab['AutoClass'] > 0]
Completed in 2.3 sec
| MatchID | Filter | GroupID | SubGroupID | RA | Dec | AutoClass | ExpertClass | VarQualFlag | FilterDetFlag | NumLC | MeanMag | MeanCorrMag | MAD | Chi2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| int64 | str11 | int64 | int64 | float64 | float64 | int64 | int64 | str5 | int64 | int64 | float64 | float64 | float64 | float64 |
| 12131288 | ACS_F475W | 69810 | -5 | 16.095659 | 2.161246 | 1 | 1 | BACAA | 1 | 12 | 25.248 | 25.250 | 0.1296 | 11.8544 |
| 12131288 | ACS_F814W | 69810 | -5 | 16.095659 | 2.161246 | 1 | 1 | AAAAC | 0 | 12 | 25.215 | 25.217 | 0.0611 | 2.3024 |
| 82653722 | ACS_F475W | 69810 | -5 | 16.097239 | 2.162066 | 2 | 1 | AACAA | 1 | 12 | 25.237 | 25.238 | 0.2312 | 64.6089 |
| 82653722 | ACS_F814W | 69810 | -5 | 16.097239 | 2.162066 | 2 | 1 | BACAA | 1 | 12 | 25.069 | 25.070 | 0.1416 | 20.4986 |
| 100437228 | ACS_F475W | 69810 | -5 | 16.111309 | 2.160908 | 2 | 1 | ABCAA | 1 | 12 | 23.249 | 23.249 | 0.1215 | 1231.5608 |
| 100437228 | ACS_F814W | 69810 | -5 | 16.111309 | 2.160908 | 2 | 1 | ABCAA | 1 | 12 | 22.850 | 22.850 | 0.0719 | 329.2444 |
| 4358745 | ACS_F475W | 69810 | -5 | 16.111961 | 2.157844 | 1 | 2 | AACAA | 1 | 7 | 26.108 | 26.111 | 0.1011 | 44.0548 |
| 78217904 | ACS_F475W | 69810 | -5 | 16.110355 | 2.162592 | 2 | 1 | AACAA | 1 | 9 | 25.374 | 25.375 | 0.4343 | 44.1083 |
| 78217904 | ACS_F814W | 69810 | -5 | 16.110355 | 2.162592 | 2 | 1 | AACAB | 1 | 9 | 25.189 | 25.189 | 0.1804 | 11.1780 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 65517209 | ACS_F475W | 69810 | -5 | 16.140654 | 2.147003 | 1 | 2 | AABAB | 0 | 12 | 23.228 | 23.229 | 0.0220 | 57.1200 |
| 65517209 | ACS_F814W | 69810 | -5 | 16.140654 | 2.147003 | 1 | 2 | BACAC | 1 | 12 | 22.374 | 22.376 | 0.0439 | 62.7181 |
| 48562344 | ACS_F475W | 69810 | -5 | 16.147528 | 2.147174 | 1 | 1 | AACAA | 1 | 12 | 25.381 | 25.381 | 0.0959 | 9.3829 |
| 48562344 | ACS_F814W | 69810 | -5 | 16.147528 | 2.147174 | 1 | 1 | AAAAC | 0 | 12 | 25.312 | 25.313 | 0.0572 | 1.9951 |
| 31257941 | ACS_F475W | 69810 | -5 | 16.107393 | 2.128815 | 2 | 1 | AACAA | 1 | 12 | 23.168 | 23.168 | 0.0664 | 3751.2152 |
| 31257941 | ACS_F814W | 69810 | -5 | 16.107393 | 2.128815 | 2 | 1 | AACAA | 1 | 12 | 22.885 | 22.887 | 0.0862 | 814.8062 |
| 14005460 | ACS_F475W | 69810 | -5 | 16.109657 | 2.127282 | 2 | 1 | AACCA | 1 | 12 | 25.470 | 25.470 | 0.1774 | 56.3907 |
| 14005460 | ACS_F814W | 69810 | -5 | 16.109657 | 2.127282 | 2 | 1 | AACAA | 1 | 10 | 25.248 | 25.250 | 0.1241 | 16.0616 |
| 57557150 | ACS_F475W | 69810 | -5 | 16.108461 | 2.128060 | 2 | 1 | AACAA | 1 | 12 | 25.319 | 25.319 | 0.1391 | 18.9906 |
| 57557150 | ACS_F814W | 69810 | -5 | 16.108461 | 2.128060 | 2 | 1 | AABAC | 1 | 12 | 25.319 | 25.320 | 0.0877 | 4.2321 |
Description of the variable classification columns #
Several of the table columns have information on the variability.
The columns
AutoClassandExpertClasshave summary information on the variability for a givenMatchIDobject.AutoClass: Classification as provided by the system: 0=constant 1=single filter variable candidate (SFVC) 2=multi-filter variable candidate (MFVC)ExpertClass: Classification as provided by expert: 0=not classified by expert, 1=high confidence variable, 2=probable variable, 4=possible artifact
The columns
MADandChi2are variability indices using the median absolute deviation and the \(\chi^2\) parameter for the given filter.The column
VarQualFlagis a variability quality flag (see Section 5 of the paper). The five letters correspond to CI, D, MagerrAper2, MagAper2-MagAuto, p2p; AAAAA corresponds to the highest quality flag.The column
FilterDetFlagis the filter detection flag: 1=source is variable in this filter, 0=source is not variable in this filter.
See the HCV paper by Bonanos et al. (2019, AAp) for more details on the computation and meaning of these quantities.
Find objects with measurements in both F475W and F814W#
This could be done in a SQL query through the CasJobs interface. Here we use the Astropy.table.join function instead.
# the only key needed to do the join is MatchID, but we include other common columns
# so that join includes only one copy of them
jtab = join(tab[tab['Filter'] == 'ACS_F475W'], tab[tab['Filter'] == 'ACS_F814W'],
keys=['MatchID', 'GroupID', 'SubGroupID', 'RA', 'Dec', 'AutoClass', 'ExpertClass'],
table_names=['f475', 'f814'])
print(len(jtab), "matched F475W+F814W objects")
jtab[jtab['AutoClass'] > 0]
17090 matched F475W+F814W objects
| MatchID | Filter_f475 | GroupID | SubGroupID | RA | Dec | AutoClass | ExpertClass | VarQualFlag_f475 | FilterDetFlag_f475 | NumLC_f475 | MeanMag_f475 | MeanCorrMag_f475 | MAD_f475 | Chi2_f475 | Filter_f814 | VarQualFlag_f814 | FilterDetFlag_f814 | NumLC_f814 | MeanMag_f814 | MeanCorrMag_f814 | MAD_f814 | Chi2_f814 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| int64 | str11 | int64 | int64 | float64 | float64 | int64 | int64 | str5 | int64 | int64 | float64 | float64 | float64 | float64 | str11 | str5 | int64 | int64 | float64 | float64 | float64 | float64 |
| 96457 | ACS_F475W | 69810 | -5 | 16.141516 | 2.177815 | 2 | 1 | AACAA | 1 | 12 | 23.192 | 23.192 | 0.0686 | 424.7097 | ACS_F814W | AAAAC | 1 | 12 | 22.946 | 22.947 | 0.0402 | 77.5733 |
| 813653 | ACS_F475W | 69810 | -5 | 16.128353 | 2.160147 | 1 | 4 | AAAAC | 0 | 10 | 25.508 | 25.507 | 0.0243 | 0.2945 | ACS_F814W | BACAB | 1 | 11 | 24.906 | 24.908 | 0.0795 | 8.5797 |
| 1012692 | ACS_F475W | 69810 | -5 | 16.134809 | 2.144720 | 2 | 1 | AACAA | 1 | 7 | 25.439 | 25.438 | 0.1446 | 17.9867 | ACS_F814W | AABAB | 1 | 8 | 25.208 | 25.210 | 0.1152 | 6.6471 |
| 1085386 | ACS_F475W | 69810 | -5 | 16.118544 | 2.160845 | 1 | 4 | AAAAC | 0 | 11 | 24.351 | 24.352 | 0.0174 | 3.1311 | ACS_F814W | BABBB | 1 | 11 | 23.476 | 23.476 | 0.0697 | 40.7630 |
| 1286857 | ACS_F475W | 69810 | -5 | 16.119205 | 2.184252 | 1 | 2 | AABAB | 1 | 12 | 23.137 | 23.138 | 0.0477 | 53.2282 | ACS_F814W | AAAAC | 0 | 12 | 21.073 | 21.075 | 0.0128 | 46.8982 |
| 1309271 | ACS_F475W | 69810 | -5 | 16.130571 | 2.152512 | 2 | 1 | AACAA | 1 | 12 | 25.347 | 25.348 | 0.1399 | 20.0434 | ACS_F814W | AAAAC | 1 | 12 | 25.043 | 25.044 | 0.0804 | 5.2954 |
| 1479646 | ACS_F475W | 69810 | -5 | 16.120852 | 2.152737 | 1 | 2 | CACAA | 0 | 12 | 23.691 | 23.692 | 0.0332 | 41.9525 | ACS_F814W | AABAB | 1 | 12 | 22.501 | 22.503 | 0.0362 | 68.2414 |
| 1661315 | ACS_F475W | 69810 | -5 | 16.110571 | 2.143526 | 1 | 4 | AACAB | 1 | 12 | 25.220 | 25.221 | 0.0780 | 5.8648 | ACS_F814W | AAAAC | 0 | 12 | 25.887 | 25.889 | 0.0595 | 0.8037 |
| 1826474 | ACS_F475W | 69810 | -5 | 16.101532 | 2.171855 | 1 | 2 | AAAAC | 0 | 11 | 25.735 | 25.737 | 0.0259 | 0.5195 | ACS_F814W | BACAB | 1 | 11 | 24.889 | 24.890 | 0.0822 | 9.2131 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 102132800 | ACS_F475W | 69810 | -5 | 16.126160 | 2.145442 | 2 | 1 | AACAA | 1 | 12 | 23.691 | 23.692 | 0.0750 | 129.5717 | ACS_F814W | AACBA | 1 | 12 | 24.503 | 24.505 | 0.1038 | 27.1660 |
| 102239423 | ACS_F475W | 69810 | -5 | 16.138706 | 2.155652 | 1 | 2 | AABAA | 1 | 12 | 22.810 | 22.811 | 0.0982 | 307.5226 | ACS_F814W | AABAA | 0 | 12 | 22.735 | 22.737 | 0.0382 | 96.9001 |
| 103232694 | ACS_F475W | 69810 | -5 | 16.107565 | 2.174399 | 1 | 4 | AAAAC | 0 | 11 | 22.422 | 22.422 | 0.0060 | 1.7118 | ACS_F814W | AAAAC | 1 | 11 | 22.425 | 22.426 | 0.0335 | 27.9930 |
| 104300195 | ACS_F475W | 69810 | -5 | 16.124981 | 2.171772 | 2 | 1 | AACAA | 1 | 12 | 25.540 | 25.541 | 0.1054 | 58.7587 | ACS_F814W | AACAA | 1 | 12 | 25.382 | 25.384 | 0.1217 | 9.4811 |
| 105173757 | ACS_F475W | 69810 | -5 | 16.133703 | 2.184506 | 2 | 1 | AAAAA | 1 | 12 | 21.372 | 21.372 | 0.1589 | 2810.1572 | ACS_F814W | AACAA | 1 | 12 | 22.240 | 22.242 | 0.1825 | 829.2399 |
| 106466795 | ACS_F475W | 69810 | -5 | 16.127056 | 2.166390 | 1 | 1 | AACAA | 1 | 12 | 25.357 | 25.358 | 0.1425 | 13.4065 | ACS_F814W | AAAAC | 0 | 12 | 25.257 | 25.259 | 0.0462 | 2.8032 |
| 106640363 | ACS_F475W | 69810 | -5 | 16.135796 | 2.149099 | 1 | 2 | CACAA | 1 | 8 | 25.577 | 25.579 | 0.1161 | 5.8168 | ACS_F814W | AABAB | 0 | 9 | 24.944 | 24.946 | 0.0661 | 8.3312 |
| 106843213 | ACS_F475W | 69810 | -5 | 16.110342 | 2.150373 | 1 | 4 | CACCB | 0 | 12 | 23.691 | 23.691 | 0.0269 | 30.7690 | ACS_F814W | CACBA | 1 | 12 | 24.429 | 24.431 | 0.0710 | 25.8158 |
| 107834538 | ACS_F475W | 69810 | -5 | 16.107105 | 2.160084 | 1 | 1 | AABAC | 1 | 12 | 25.400 | 25.401 | 0.0818 | 3.4254 | ACS_F814W | AAAAC | 0 | 12 | 25.128 | 25.129 | 0.0578 | 1.7916 |
| 108048053 | ACS_F475W | 69810 | -5 | 16.150572 | 2.142590 | 1 | 2 | AACCA | 1 | 10 | 25.297 | 25.297 | 0.0697 | 22.9085 | ACS_F814W | AAAAC | 0 | 11 | 24.544 | 24.546 | 0.0273 | 1.6361 |
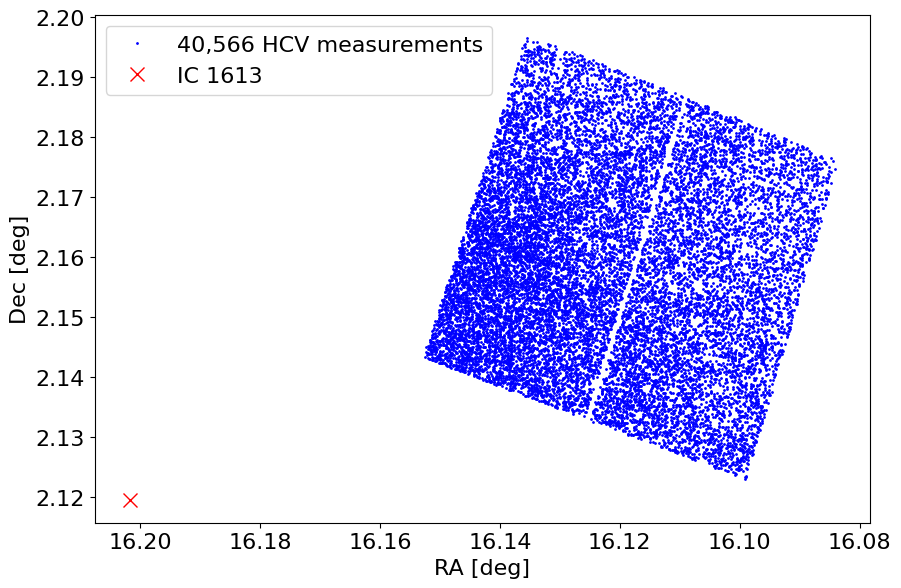
Plot object positions on the sky #
We mark the galaxy center as well. Note that this field is in the outskirts of IC 1613. The 0.5 degree search radius (which is the maximum allowed in the API) allows finding these objects.
fig, ax = plt.subplots(figsize=(10, 10))
ax.plot('RA', 'Dec', 'bo', markersize=1, label=f'{len(tab):,} HCV measurements', data=jtab)
ax.plot(ra_ic1613, dec_ic1613, 'rx', label=target, markersize=10)
ax.invert_xaxis()
ax.set(aspect='equal', xlabel='RA [deg]', ylabel='Dec [deg]')
ax.legend(loc='best')
<matplotlib.legend.Legend at 0x7eff61ad7590>
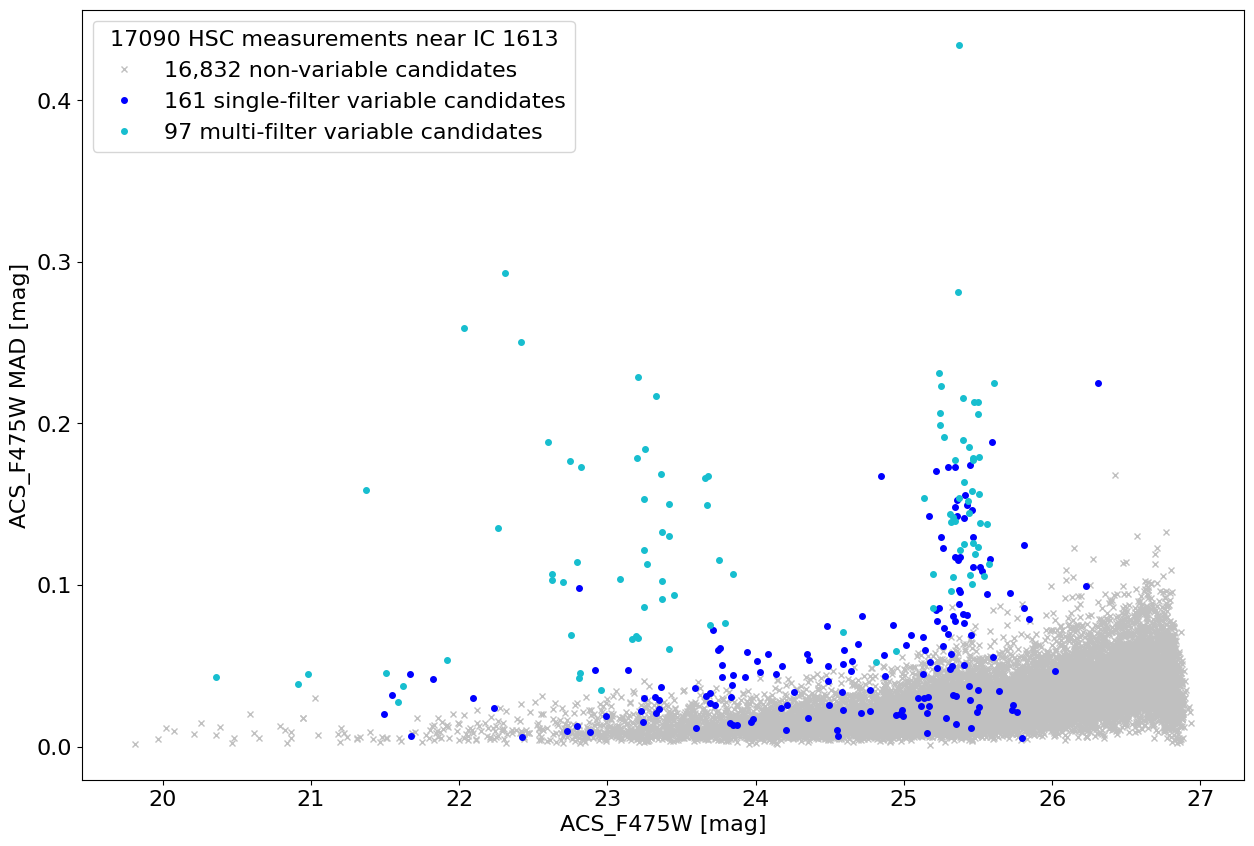
Plot HCV MAD variability index versus magnitude in F475W #
The median absolute deviation variability index is used by the HCV to identify variables. It measures the scatter among the multi-epoch measurements. Some scatter is expected from noise (which increases for fainter objects). Objects with MAD values that are high are likely to be variable.
This plots single-filter and multi-filter variable candidates (SFVC and MFVC) in different colors. Note that variable objects with low F475W MAD values are variable in a different filter (typically F814W in this field).
This plot is similar to the upper panel of Figure 4 in Bonanos et al. (2019, AAp).
# define plot parameter lists
auto_class = np.unique(jtab['AutoClass'])
markers = ['x', 'o', 'o']
colors = ['silver', 'blue', 'tab:cyan']
labels = ['non-', 'single-filter ', 'multi-filter ']
fig, ax = plt.subplots(figsize=(15, 10))
for ac, marker, color, label in zip(auto_class, markers, colors, labels):
data = jtab[jtab['AutoClass'] == ac]
ax.plot('MeanCorrMag_f475', 'MAD_f475', marker, markersize=4, color=color,
label=f'{len(data):,} {label}variable candidates', data=data)
ax.set(xlabel='ACS_F475W [mag]', ylabel='ACS_F475W MAD [mag]')
ax.legend(loc='best', title=f'{len(jtab)} HSC measurements near {target}')
<matplotlib.legend.Legend at 0x7eff61bf0b10>
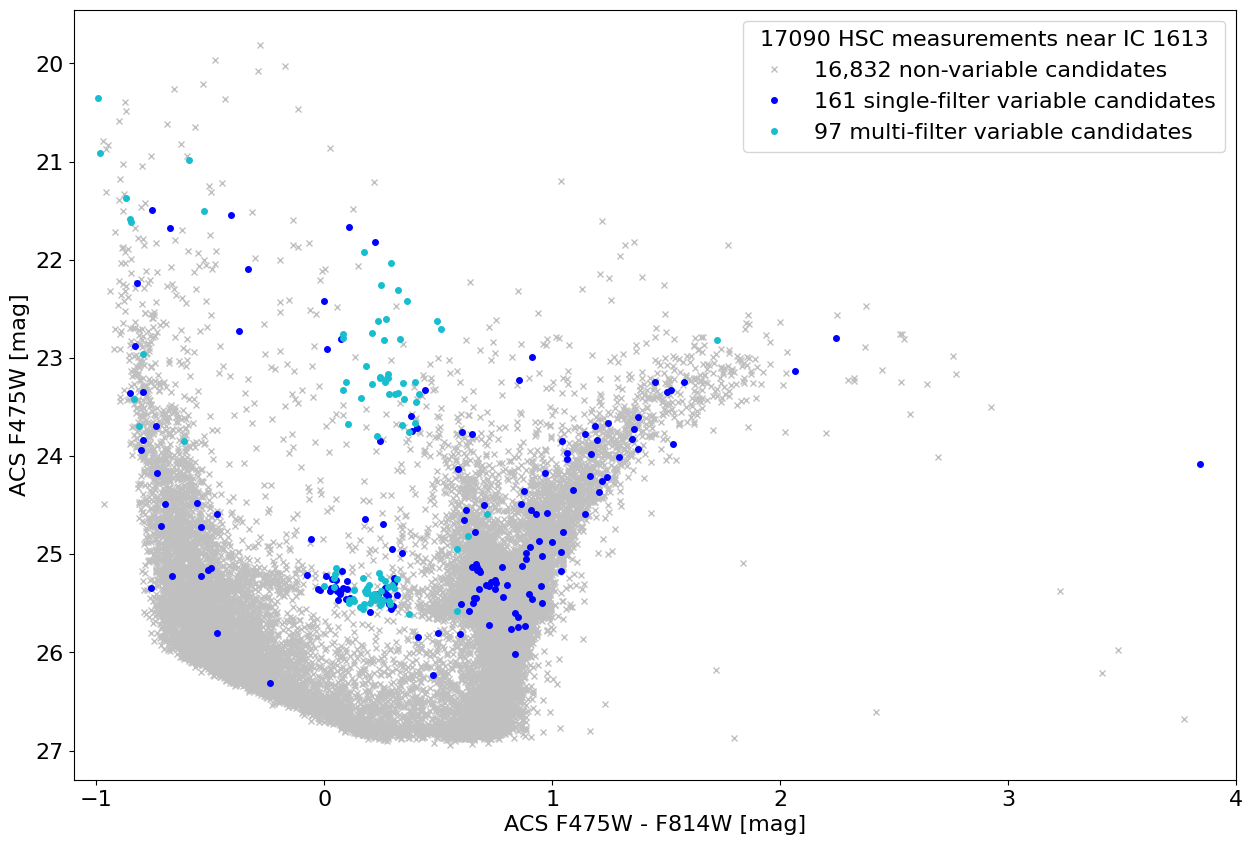
Plot variables in color-magnitude diagram #
Many of the candidate variables lie on the instability strip.
This plot is similar to the lower panel of Figure 4 in Bonanos et al. (2019, AAp).
# add a new column to jtab
jtab['MCMf475-MCMf814'] = jtab['MeanCorrMag_f475'] - jtab['MeanCorrMag_f814']
fig, ax = plt.subplots(figsize=(15, 10))
# uses same plot parameters defined in the previous plot
for ac, marker, color, label in zip(auto_class, markers, colors, labels):
data = jtab[jtab['AutoClass'] == ac]
ax.plot('MCMf475-MCMf814', 'MeanCorrMag_f475', marker, markersize=4, color=color,
label=f'{len(data):,} {label}variable candidates', data=data)
ax.invert_yaxis()
ax.set(xlim=(-1.1, 4), xlabel='ACS F475W - F814W [mag]', ylabel='ACS F475W [mag]')
ax.legend(loc='best', title=f'{len(jtab)} HSC measurements near {target}')
<matplotlib.legend.Legend at 0x7eff601de2d0>
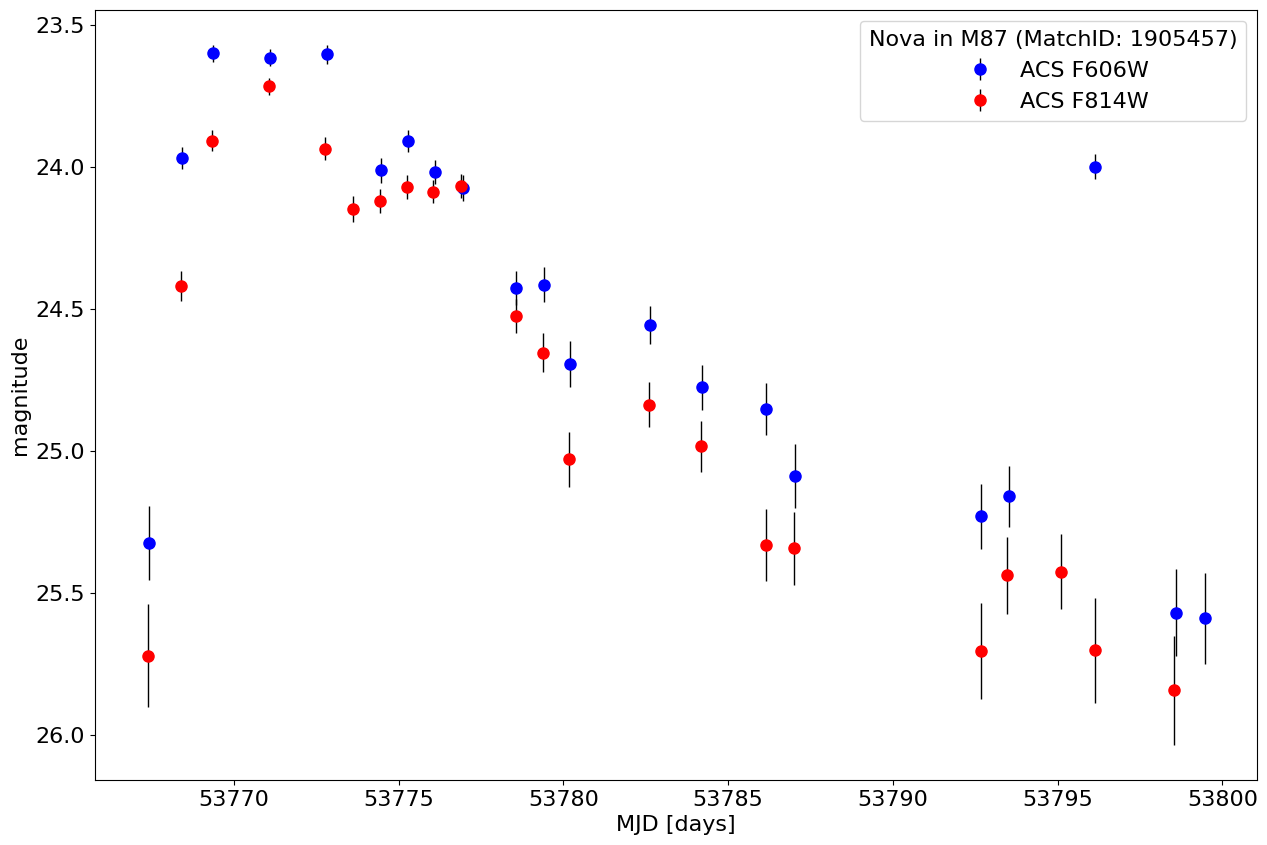
Get a light curve for a nova in M87 #
Extract light curve for a given MatchID #
Note that the MatchID could be determined by positional searches, filtering the catalog, etc. This object comes from the top left panel of Figure 9 in Bonanos et al. (2019, AAp).
matchid = 1905457
t0 = time.time()
# get light curves for F606W and F814W
nova_606 = ascii.read(hcvsearch(table='hcv', MatchID=matchid, Filter='ACS_F606W'))
print(f"{(time.time()-t0):.1f} sec: retrieved {len(nova_606)} F606W measurements")
nova_814 = ascii.read(hcvsearch(table='hcv', MatchID=matchid, Filter='ACS_F814W'))
print(f"{(time.time()-t0):.1f} sec: retrieved {len(nova_814)} F814W measurements")
# get the object RA and Dec as well
nova_tab = ascii.read(hcvsearch(table='hcvsummary', MatchID=matchid, Filter='ACS_F814W'))
print(f"{(time.time()-t0):.1f} sec: retrieved object info")
nova_606
0.1 sec: retrieved 21 F606W measurements
0.3 sec: retrieved 22 F814W measurements
0.4 sec: retrieved object info
| MatchID | Filter | MJD | ImageName | Mag | CorrMag | MagErr | CI | D |
|---|---|---|---|---|---|---|---|---|
| int64 | str9 | float64 | str26 | float64 | float64 | float64 | float64 | float64 |
| 1905457 | ACS_F606W | 53767.4197952871 | hst_10543_29_acs_wfc_f606w | 25.327 | 25.3267132802993 | 0.1305 | 0.840648114681244 | 13.499119758606 |
| 1905457 | ACS_F606W | 53768.4190663833 | hst_10543_30_acs_wfc_f606w | 23.9694 | 23.9676109802196 | 0.0394 | 1.04379630088806 | 11.9895544052124 |
| 1905457 | ACS_F606W | 53769.3576541713 | hst_10543_31_acs_wfc_f606w | 23.6005 | 23.6000842124737 | 0.0306 | 0.974166631698608 | 9.30478286743164 |
| 1905457 | ACS_F606W | 53771.1017052617 | hst_10543_33_acs_wfc_f606w | 23.6105 | 23.6157510517543 | 0.030300001 | 0.96657407283783 | 2.96933674812317 |
| 1905457 | ACS_F606W | 53772.8098534283 | hst_10543_35_acs_wfc_f606w | 23.621799 | 23.602993885395 | 0.0328 | 0.992037057876587 | 4.45478820800781 |
| 1905457 | ACS_F606W | 53774.4746564087 | hst_10543_37_acs_wfc_f606w | 24.015499 | 24.0123868023881 | 0.042599998 | 1.0246297121048 | 3.4874792098999 |
| 1905457 | ACS_F606W | 53775.2799112014 | hst_10543_38_acs_wfc_f606w | 23.9037 | 23.9077547341058 | 0.0381 | 0.985185205936432 | 3.49740219116211 |
| 1905457 | ACS_F606W | 53776.0893441574 | hst_10543_39_acs_wfc_f606w | 24.015499 | 24.0182108840315 | 0.0414 | 1.05314815044403 | 8.44466972351074 |
| 1905457 | ACS_F606W | 53776.9439852673 | hst_10543_40_acs_wfc_f606w | 24.065701 | 24.0743889490328 | 0.044599999 | 1.24157404899597 | 7.6749701499939 |
| 1905457 | ACS_F606W | 53778.562434162 | hst_10543_42_acs_wfc_f606w | 24.430799 | 24.4274937224049 | 0.059500001 | 1.07425928115845 | 3.26662158966064 |
| 1905457 | ACS_F606W | 53779.4097260174 | hst_10543_43_acs_wfc_f606w | 24.415899 | 24.4150584573105 | 0.062600002 | 0.965277791023254 | 2.09669971466064 |
| 1905457 | ACS_F606W | 53780.2090778507 | hst_10543_44_acs_wfc_f606w | 24.697599 | 24.6944838119623 | 0.080499999 | 0.810648143291473 | 6.5630521774292 |
| 1905457 | ACS_F606W | 53782.61915897 | hst_10543_47_acs_wfc_f606w | 24.560801 | 24.5570748994592 | 0.065399997 | 1.09907412528992 | 2.88692712783813 |
| 1905457 | ACS_F606W | 53784.2176541714 | hst_10543_73_acs_wfc_f606w | 24.7827 | 24.7770110702267 | 0.079000004 | 0.888148188591003 | 3.16040587425232 |
| 1905457 | ACS_F606W | 53786.1563230369 | hst_10543_86_acs_wfc_f606w | 24.9091 | 24.8532684587691 | 0.0902 | 1.03777778148651 | 8.54914951324463 |
| 1905457 | ACS_F606W | 53787.0225386124 | hst_10543_92_acs_wfc_f606w | 25.114599 | 25.0878230960564 | 0.1127 | 0.924444437026978 | 4.14372444152832 |
| 1905457 | ACS_F606W | 53792.6850963715 | hst_10543_49_acs_wfc_f606w | 25.228001 | 25.231832236643 | 0.1147 | 1.14425933361053 | 11.9895496368408 |
| 1905457 | ACS_F606W | 53793.5260915786 | hst_10543_a1_acs_wfc_f606w | 25.153601 | 25.1604359861786 | 0.1071 | 0.925648152828217 | 7.5528678894043 |
| 1905457 | ACS_F606W | 53796.1486378878 | hst_10543_b8_acs_wfc_f606w | 24.0172 | 23.9985920051837 | 0.0436 | 1.51175928115845 | 10.1193161010742 |
| 1905457 | ACS_F606W | 53798.5892174062 | hst_10543_50_acs_wfc_f606w | 25.563601 | 25.5708965234736 | 0.15350001 | 0.953240752220154 | 12.9010400772095 |
| 1905457 | ACS_F606W | 53799.4608942058 | hst_10543_c4_acs_wfc_f606w | 25.5895 | 25.5908707417737 | 0.1602 | 0.92981481552124 | 5.97602415084839 |
fig, ax = plt.subplots(figsize=(15, 10))
ax.errorbar(x='MJD', y='CorrMag', yerr='MagErr', fmt='ob', ecolor='k', elinewidth=1, markersize=8, label='ACS F606W', data=nova_606)
ax.errorbar(x='MJD', y='CorrMag', yerr='MagErr', fmt='or', ecolor='k', elinewidth=1, markersize=8, label='ACS F814W', data=nova_814)
ax.invert_yaxis()
ax.set(xlabel='MJD [days]', ylabel='magnitude')
ax.legend(loc='best', title=f'Nova in M87 (MatchID: {matchid})')
<matplotlib.legend.Legend at 0x7eff6027cb50>
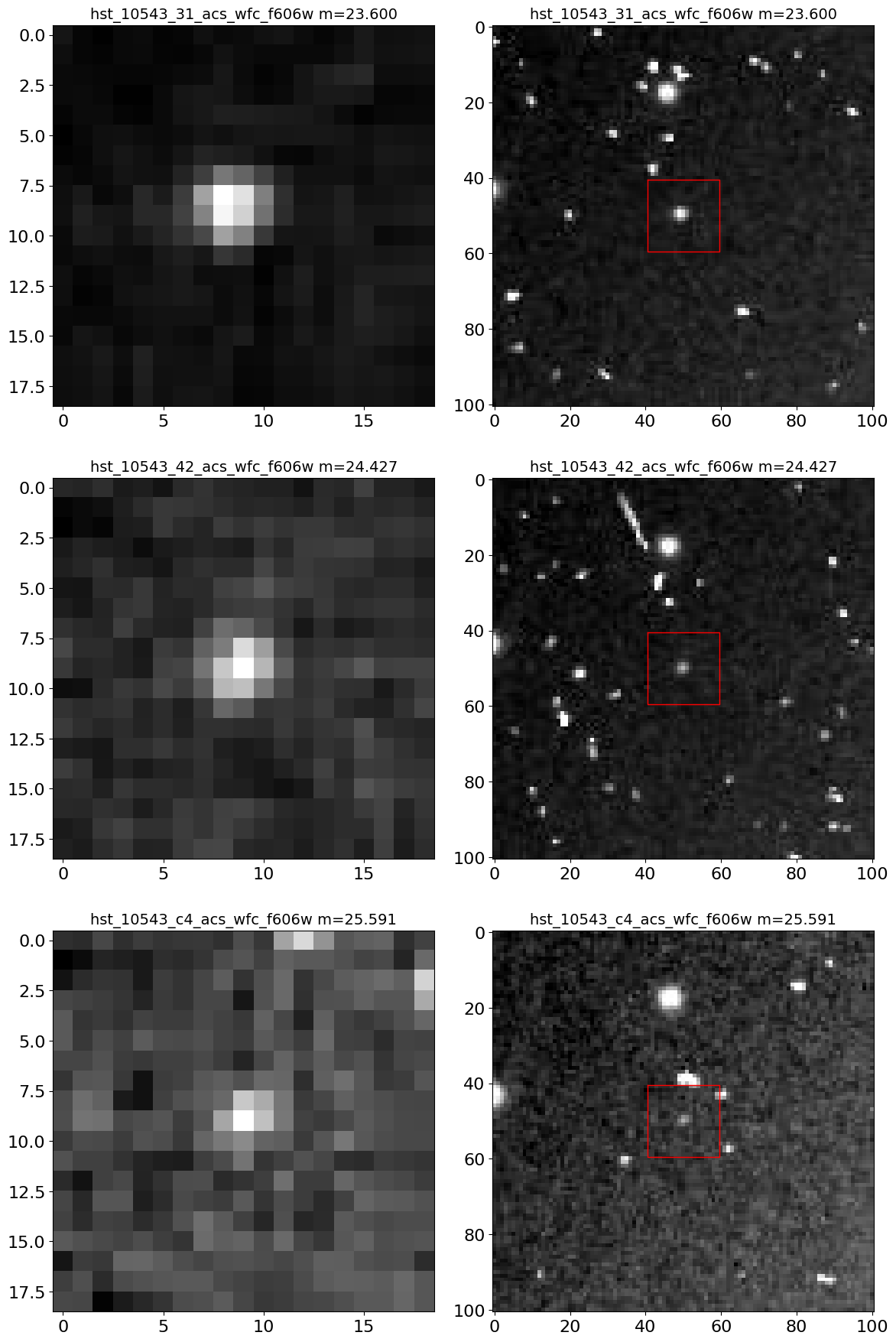
Get HLA image cutouts for the nova #
The Hubble Legacy Archive (HLA) images were the source of the measurements in the HSC and HCV, and it can be useful to look at the images. Examination of the images can be useful to identified cosmic-ray contamination and other possible image artifacts. In this case, no issues are seen, so the light curve is reliable.
Note that the ACS F606W images of M87 have only a single exposure, so they do have cosmic ray contamination. The accompanying F814W images have multiple exposures, allowing CRs to be removed. In this case the F814W combined image is used to find objects, while the F606W exposure is used only for photometry. That reduces the effects of F606W CRs on the catalog but it is still a good idea to confirm the quality of the images.
The get_hla_cutout function reads a single cutout image (as a JPEG grayscale image) and returns a PIL image object. See the documentation on the fitscut image cutout service for more information on the web service being used.
def get_hla_cutout(imagename, ra, dec, size=33, autoscale=99.5, asinh=True, zoom=1):
"""Get JPEG cutout for an image"""
url = "https://hla.stsci.edu/cgi-bin/fitscut.cgi"
r = requests.get(url, params=dict(ra=ra, dec=dec, size=size,
format="jpeg", red=imagename, autoscale=autoscale, asinh=asinh, zoom=zoom))
im = Image.open(BytesIO(r.content))
return im
# sort images by magnitude from brightest to faintest
phot = nova_606
isort = np.argsort(phot['CorrMag'])
# select the brightest, median and faintest magnitudes
ind = [isort[0], isort[len(isort)//2], isort[-1]]
# we plot zoomed-in and zoomed-out views side-by-side for each selected image
nim = len(ind)*2
ncols = 2 # images per row
nrows = (nim+ncols-1)//ncols
imsize1 = 19
imsize2 = 101
mra = nova_tab['RA'][0]
mdec = nova_tab['Dec'][0]
# define figure and axes
fig, axes = plt.subplots(nrows, ncols, figsize=(12, (12/ncols)*nrows), tight_layout=True)
t0 = time.time()
# iterate through each set of two subplots in axes
for (ax1, ax2), k in zip(axes, ind):
# get the images
im1 = get_hla_cutout(phot['ImageName'][k], mra, mdec, size=imsize1)
im2 = get_hla_cutout(phot['ImageName'][k], mra, mdec, size=imsize2)
# plot left column
ax1.imshow(im1, origin="upper", cmap="gray")
ax1.set_title(f"{phot['ImageName'][k]} m={phot['CorrMag'][k]:.3f}", fontsize=14)
# plot right column
ax2.imshow(im2, origin="upper", cmap="gray")
xbox = np.array([-1, 1])*imsize1/2 + (imsize2-1)//2
ax2.plot(xbox[[0, 1, 1, 0, 0]], xbox[[0, 0, 1, 1, 0]], 'r-', linewidth=1)
ax2.set_title(f"{phot['ImageName'][k]} m={phot['CorrMag'][k]:.3f}", fontsize=14)
print(f"{(time.time()-t0):.1f} s: got {nrows*ncols} cutouts")
4.8 s: got 6 cutouts
Compare the HCV automatic classification to expert validations #
The HCV includes an automatic classification AutoClass for candidate variables as well as an expert validation for some fields that were selected for visual examination. For this example, we select all the objects in the HCV that have expert classification information.
t0 = time.time()
# get data for objects with an expert validation
constraints = {"ExpertClass.gte": 1}
tab = ascii.read(hcvsearch(table="hcvsummary", **constraints))
print(f"Retrieved {len(tab)} rows in {(time.time()-t0):.1f} sec")
# clean up the output format
tab['MeanMag'].format = "{:.3f}"
tab['MeanCorrMag'].format = "{:.3f}"
tab['MAD'].format = "{:.4f}"
tab['Chi2'].format = "{:.4f}"
tab['RA'].format = "{:.6f}"
tab['Dec'].format = "{:.6f}"
# tab includes 1 row for each filter (so multiple rows for objects with multiple filters)
# get an array that has only one row per object
mval, uindex = np.unique(tab['MatchID'], return_index=True)
utab = tab[uindex]
print(f"{len(utab)} unique MatchIDs in table")
tab
Retrieved 31258 rows in 0.8 sec
13533 unique MatchIDs in table
| MatchID | Filter | GroupID | SubGroupID | RA | Dec | AutoClass | ExpertClass | VarQualFlag | FilterDetFlag | NumLC | MeanMag | MeanCorrMag | MAD | Chi2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| int64 | str11 | int64 | int64 | float64 | float64 | int64 | int64 | str5 | int64 | int64 | float64 | float64 | float64 | float64 |
| 875 | ACS_F435W | 1040153 | -5 | 64.149673 | -24.110353 | 2 | 2 | AAAAA | 0 | 13 | 24.166 | 24.166 | 0.0384 | 7.1169 |
| 875 | ACS_F606W | 1040153 | -5 | 64.149673 | -24.110353 | 2 | 2 | AAAAC | 0 | 9 | 22.836 | 22.835 | 0.0349 | 81.3676 |
| 875 | ACS_F814W | 1040153 | -5 | 64.149673 | -24.110353 | 2 | 2 | AAAAA | 0 | 23 | 22.156 | 22.156 | 0.0325 | 141.7171 |
| 875 | WFC3_F105W | 1040153 | -5 | 64.149673 | -24.110353 | 2 | 2 | CAAAB | 1 | 14 | 21.843 | 21.843 | 0.0503 | 223.4961 |
| 875 | WFC3_F125W | 1040153 | -5 | 64.149673 | -24.110353 | 2 | 2 | CBCCA | 1 | 6 | 21.813 | 21.814 | 0.0655 | 792.8662 |
| 875 | WFC3_F140W | 1040153 | -5 | 64.149673 | -24.110353 | 2 | 2 | AAAAA | 0 | 6 | 21.705 | 21.704 | 0.0205 | 127.6242 |
| 875 | WFC3_F160W | 1040153 | -5 | 64.149673 | -24.110353 | 2 | 2 | BABAA | 1 | 13 | 21.623 | 21.624 | 0.0322 | 112.8544 |
| 2006 | WFPC2_F555W | 521507 | -5 | 268.112152 | -17.684282 | 2 | 2 | AAAAC | 1 | 7 | 21.811 | 21.821 | 0.1545 | 85.2812 |
| 2006 | WFPC2_F814W | 521507 | -5 | 268.112152 | -17.684282 | 2 | 2 | AAAAA | 1 | 7 | 20.513 | 20.519 | 0.0988 | 105.2348 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 108116850 | ACS_F475W | 1045904 | 85 | 11.627593 | 42.061874 | 1 | 1 | AAAAA | 0 | 5 | 24.772 | 24.774 | 0.0498 | 52.0622 |
| 108116850 | ACS_F814W | 1045904 | 85 | 11.627593 | 42.061874 | 1 | 1 | AACAA | 1 | 5 | 24.605 | 24.607 | 0.1120 | 56.7844 |
| 108127522 | ACS_F606W | 1043478 | -5 | 211.154297 | 54.521580 | 1 | 1 | AACAA | 1 | 6 | 26.786 | 26.786 | 0.1496 | 12.5680 |
| 108141967 | ACS_F606W | 1036556 | -5 | 34.188431 | -5.203189 | 1 | 4 | BAACA | 1 | 5 | 26.174 | 26.175 | 0.1806 | 5.3338 |
| 108141967 | ACS_F814W | 1036556 | -5 | 34.188431 | -5.203189 | 1 | 4 | AAAAC | 0 | 5 | 25.970 | 25.969 | 0.0561 | 0.2748 |
| 108154109 | ACS_F606W | 1084533 | -5 | 53.141266 | -27.710630 | 1 | 2 | CAAAC | 0 | 7 | 24.477 | 24.477 | 0.0161 | 3.4616 |
| 108154109 | ACS_F775W | 1084533 | -5 | 53.141266 | -27.710630 | 1 | 2 | CAAAC | 0 | 11 | 23.650 | 23.650 | 0.0588 | 2.6932 |
| 108154109 | ACS_F814W | 1084533 | -5 | 53.141266 | -27.710630 | 1 | 2 | CAAAC | 0 | 5 | 23.577 | 23.577 | 0.0037 | 2.9994 |
| 108154109 | ACS_F850LP | 1084533 | -5 | 53.141266 | -27.710630 | 1 | 2 | CAAAA | 1 | 12 | 23.455 | 23.455 | 0.0639 | 3.4468 |
| 108154109 | WFC3_F105W | 1084533 | -5 | 53.141266 | -27.710630 | 1 | 2 | AAAAC | 0 | 6 | 21.541 | 21.541 | 0.0065 | 0.4013 |
An ExpertClass value of 1 indicates that the object is confidently confirmed to be a variable; 2 means that the measurements do not have apparent problems and so the object is likely to be variable (usually the variability is too small to be obvious in the image); 4 means that the variability is likely to be the result of artifacts in the image (e.g., residual cosmic rays or diffraction spikes from nearby bright stars).
Compare the distributions for single-filter variable candidates (SFVC, AutoClass=1) and multi-filter variable candidates (MFVC, AutoClass=2). The fraction of artifacts is lower in the MFVC sample.
sfcount = np.bincount(utab['ExpertClass'][utab['AutoClass'] == 1])
mfcount = np.bincount(utab['ExpertClass'][utab['AutoClass'] == 2])
sfrat = sfcount/sfcount.sum()
mfrat = mfcount/mfcount.sum()
print("Type Variable Likely Artifact Total")
print("SFVC {:8d} {:6d} {:8d} {:5d} counts".format(sfcount[1], sfcount[2], sfcount[4], sfcount.sum()))
print("MFVC {:8d} {:6d} {:8d} {:5d} counts".format(mfcount[1], mfcount[2], mfcount[4], mfcount.sum()))
print("SFVC {:8.3f} {:6.3f} {:8.3f} {:5.3f} fraction".format(sfrat[1], sfrat[2], sfrat[4], sfrat.sum()))
print("MFVC {:8.3f} {:6.3f} {:8.3f} {:5.3f} fraction".format(mfrat[1], mfrat[2], mfrat[4], mfrat.sum()))
Type Variable Likely Artifact Total
SFVC 3323 3055 1761 8139 counts
MFVC 2101 2442 851 5394 counts
SFVC 0.408 0.375 0.216 1.000 fraction
MFVC 0.390 0.453 0.158 1.000 fraction
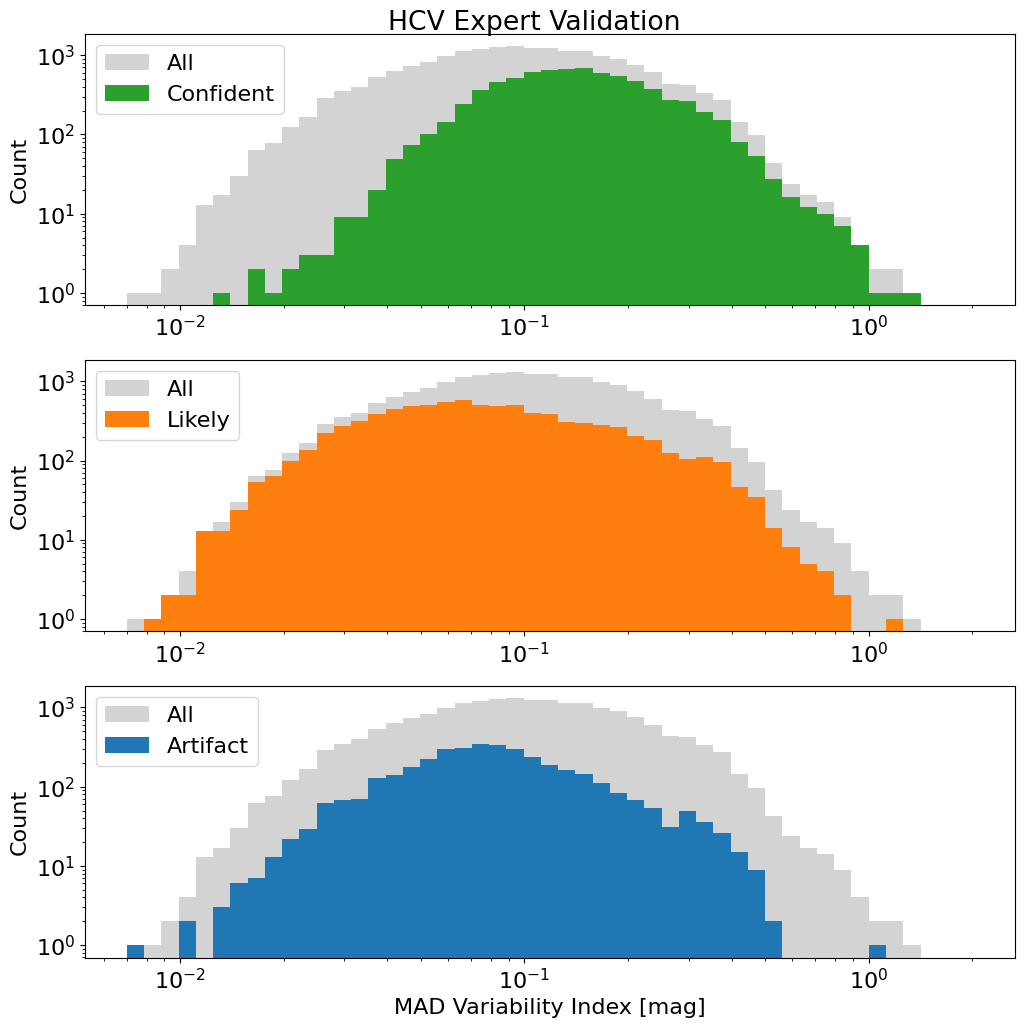
Plot the MAD variability index distribution with expert classifications #
Note that only the filters identified as variable (FilterDetFlag > 0) are included here.
This version of the plot shows the distributions for the various ExpertClass values along with, for comparison, the distribution for all objects in gray (which is identical in each panel). Most objects are classified as confident or likely variables. Objects with lower MAD values (indicating a lower amplitude of variability) are less likely to be identified as confident variables because low-level variability is more difficult to confirm via visual examination.
Data & Bins#
w = np.where(tab['FilterDetFlag'] > 0)
mad = tab['MAD'][w]
e = tab['ExpertClass'][w]
xrange = [7.e-3, 2.0]
bins = xrange[0]*(xrange[1]/xrange[0])**np.linspace(0.0, 1.0, 50)
Plots#
fig, axes = plt.subplots(3, 1, figsize=(12, 12))
labels = ['Confident', 'Likely', 'Artifact']
colors = ['C2', 'C1', 'C0']
for ax, v, label, color in zip(axes, np.unique(e), labels, colors):
ax.hist(mad, bins=bins, log=True, color='lightgray', label='All')
ax.hist(mad[e == v], bins=bins, log=True, label=label, color=color)
ax.set(xscale='log', ylabel='Count')
ax.legend(loc='upper left')
fig.suptitle('HCV Expert Validation', y=0.9)
_ = axes[2].set_xlabel('MAD Variability Index [mag]')
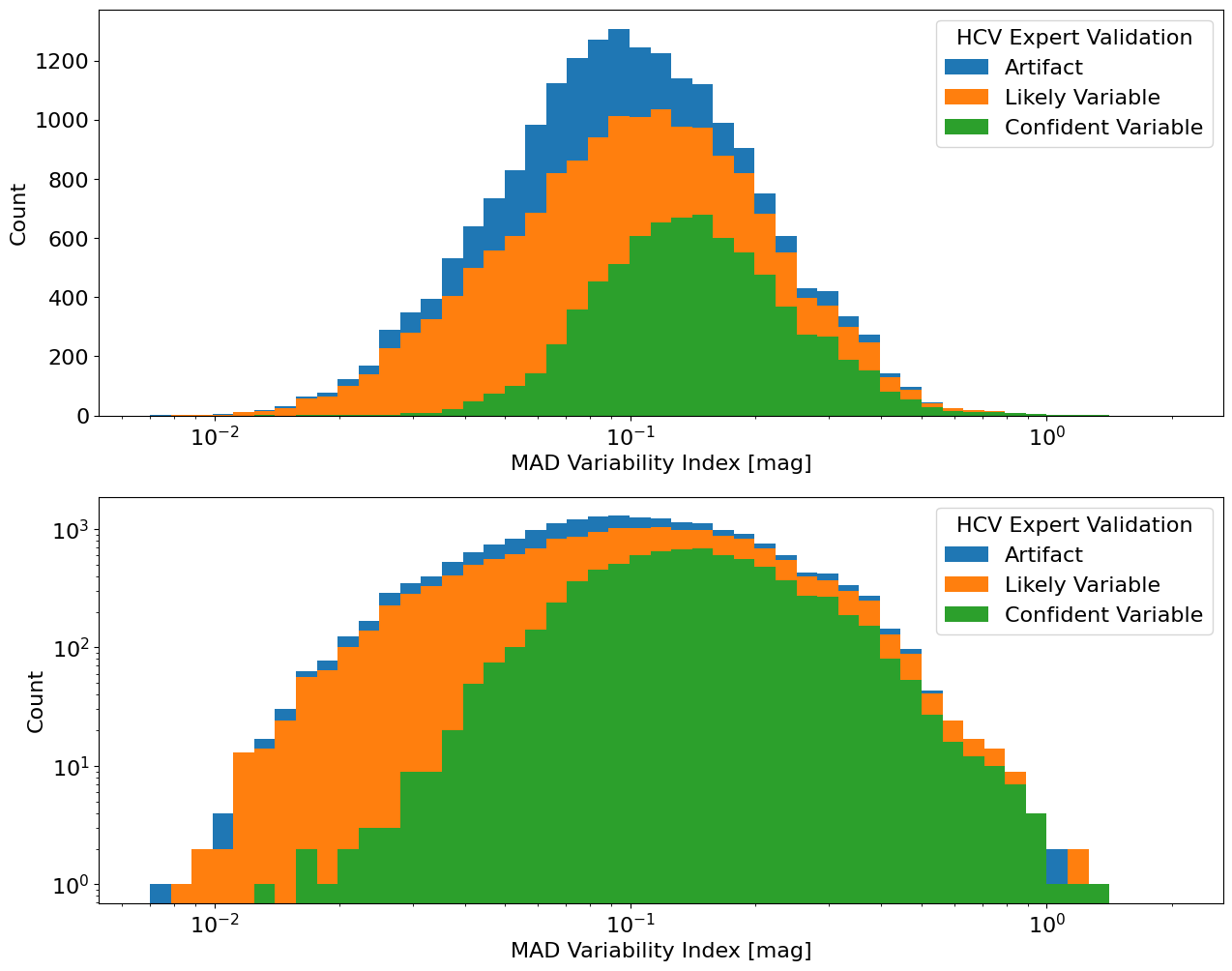
The plot below shows the same distributions, but plotted as stacked histograms. The top panel uses a linear scale on the y-axis and the bottom panel uses a log y scale.
fig, axes = plt.subplots(2, 1, figsize=(15, 12))
ylogs = [False, True]
for ax, ylog in zip(axes, ylogs):
ax.hist(mad, bins=bins, log=ylog, label='Artifact')
ax.hist(mad[e < 4], bins=bins, log=ylog, label='Likely Variable')
ax.hist(mad[e == 1], bins=bins, log=ylog, label='Confident Variable')
ax.set_xscale('log')
ax.set_xlabel('MAD Variability Index [mag]')
ax.set_ylabel('Count')
ax.legend(loc='upper right', title='HCV Expert Validation')
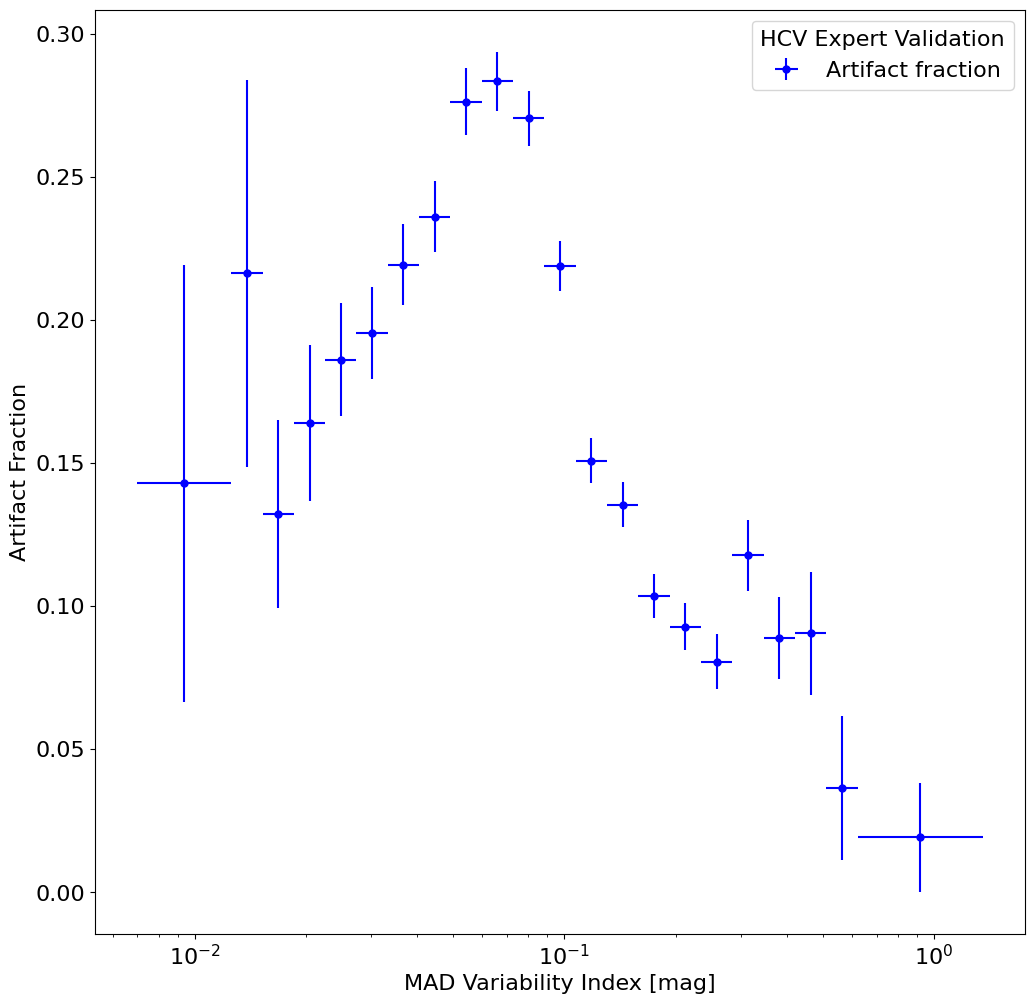
Plot the fraction of artifacts as a function of MAD variability index #
This shows how the fraction of artifacts varies with the MAD value. For larger MAD values the fraction decreases sharply, presumably because such large values are less likely to result from the usual artifacts. Interestingly, the artifact fraction also declines for smaller MAD values (MAD < 0.1 mag). Probably that happens because typical artifacts are more likely to produce strong signals than the weaker signals indicated by a low MAD value.
w = np.where(tab['FilterDetFlag'] > 0)
mad = tab['MAD'][w]
e = tab['ExpertClass'][w]
xrange = [7.e-3, 2.0]
bins = xrange[0]*(xrange[1]/xrange[0])**np.linspace(0.0, 1.0, 30)
all_count, bin_edges = np.histogram(mad, bins=bins)
artifact_count, bin_edges = np.histogram(mad[e == 4], bins=bins)
wnz = np.where(all_count > 0)[0]
nnz = len(wnz)
artifact_count = artifact_count[wnz]
all_count = all_count[wnz]
xerr = np.empty((2, nnz), dtype=float)
xerr[0] = bin_edges[wnz]
xerr[1] = bin_edges[wnz+1]
# combine bins at edge into one big bin to improve the statistics there
iz = np.where(all_count.cumsum() > 10)[0][0]
if iz > 0:
all_count[iz] += all_count[:iz].sum()
artifact_count[iz] += artifact_count[:iz].sum()
xerr[0, iz] = xerr[0, 0]
all_count = all_count[iz:]
artifact_count = artifact_count[iz:]
xerr = xerr[:, iz:]
iz = np.where(all_count[::-1].cumsum() > 40)[0][0]
if iz > 0:
all_count[-iz-1] += all_count[-iz:].sum()
artifact_count[-iz-1] = artifact_count[-iz:].sum()
xerr[1, -iz-1] = xerr[1, -1]
all_count = all_count[:-iz]
artifact_count = artifact_count[:-iz]
xerr = xerr[:, :-iz]
x = np.sqrt(xerr[0]*xerr[1])
xerr[0] = x - xerr[0]
xerr[1] = xerr[1] - x
frac = artifact_count/all_count
# error on fraction using binomial distribution (approximate)
ferr = np.sqrt(frac*(1-frac)/all_count)
Create the plot
fig, ax = plt.subplots(figsize=(12, 12))
ax.errorbar(x, frac, xerr=xerr, yerr=ferr, fmt='ob', markersize=5, label='Artifact fraction')
ax.set(xscale='log', xlabel='MAD Variability Index [mag]', ylabel='Artifact Fraction')
ax.legend(loc='upper right', title='HCV Expert Validation')
<matplotlib.legend.Legend at 0x7eff60c61c10>
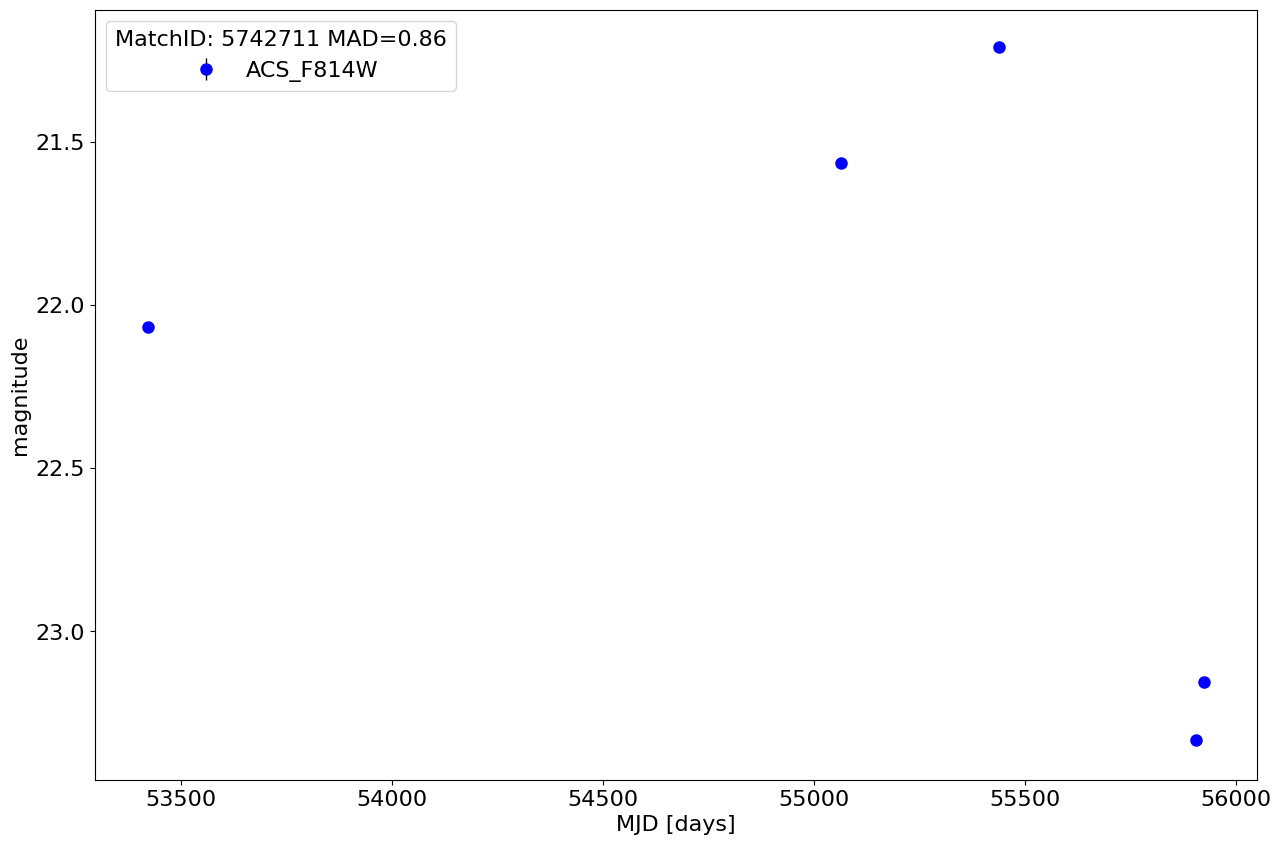
Plot light curve for the most variable high quality candidate in the HCV #
Select the candidate variable with the largest MAD value and VarQualFlag = ‘AAAAA’. To find the highest MAD value, we sort by MAD in descending order and select the first result.
constraints = {'VarQualFlag': 'AAAAA', 'sort_by': 'MAD.desc', 'pagesize': 1}
t0 = time.time()
tab = ascii.read(hcvsearch(table='hcvsummary', **constraints))
print("Completed in {:.1f} sec".format(time.time()-t0))
# clean up the output format
tab['MeanMag'].format = "{:.3f}"
tab['MeanCorrMag'].format = "{:.3f}"
tab['MAD'].format = "{:.4f}"
tab['Chi2'].format = "{:.4f}"
tab['RA'].format = "{:.6f}"
tab['Dec'].format = "{:.6f}"
print("MatchID {} has largest MAD value = {:.2f}".format(
tab['MatchID'][0], tab['MAD'][0]))
tab
Completed in 1.1 sec
MatchID 5742711 has largest MAD value = 0.86
| MatchID | Filter | GroupID | SubGroupID | RA | Dec | AutoClass | ExpertClass | VarQualFlag | FilterDetFlag | NumLC | MeanMag | MeanCorrMag | MAD | Chi2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| int64 | str9 | int64 | int64 | float64 | float64 | int64 | int64 | str5 | int64 | int64 | float64 | float64 | float64 | float64 |
| 5742711 | ACS_F814W | 1045904 | 16 | 10.928601 | 41.164295 | 1 | 0 | AAAAA | 1 | 5 | 22.264 | 22.265 | 0.8581 | 6698.4430 |
Get the light curve.
matchid = tab['MatchID'][0]
mfilter = tab['Filter'][0]
t0 = time.time()
lc = ascii.read(hcvsearch(table="hcv", MatchID=matchid, Filter=mfilter))
print(f"{(time.time()-t0):.1f} sec: retrieved {len(lc)} {mfilter} measurements")
0.2 sec: retrieved 5 ACS_F814W measurements
Plot the light curve.
fig, ax = plt.subplots(figsize=(15, 10))
ax.errorbar(x='MJD', y='CorrMag', yerr='MagErr', fmt='ob', ecolor='k', elinewidth=1, markersize=8, label=mfilter, data=lc)
ax.invert_yaxis()
ax.set(xlabel='MJD [days]', ylabel='magnitude')
ax.legend(loc='best', title=f"MatchID: {matchid} MAD={tab['MAD'][0]:.2f}")
<matplotlib.legend.Legend at 0x7eff609fe2d0>
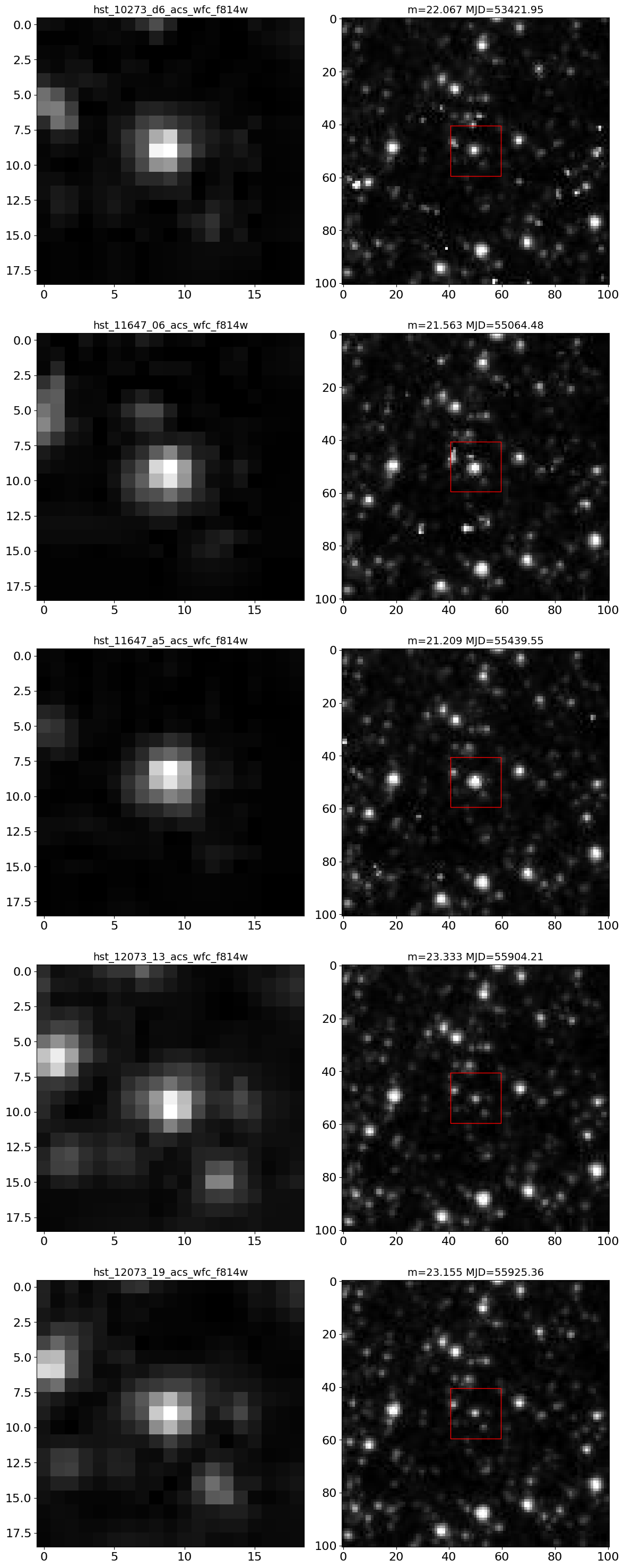
Extract cutout images for the entire light curve (since it does not have many points).
# sort images in MJD order
ind = np.argsort(lc['MJD'])
# we plot zoomed-in and zoomed-out views side-by-side for each selected image
nim = len(ind)*2
ncols = 2 # images per row
nrows = (nim+ncols-1)//ncols
imsize1 = 19
imsize2 = 101
mra = tab['RA'][0]
mdec = tab['Dec'][0]
# define figure and axes
fig, axes = plt.subplots(nrows, ncols, figsize=(12, (12/ncols)*nrows), tight_layout=True)
t0 = time.time()
# iterate through each set of two subplots in axes
for i, ((ax1, ax2), k) in enumerate(zip(axes, ind), 1):
# get the images
im1 = get_hla_cutout(lc['ImageName'][k], mra, mdec, size=imsize1)
im2 = get_hla_cutout(lc['ImageName'][k], mra, mdec, size=imsize2)
# plot left column
ax1.imshow(im1, origin="upper", cmap="gray")
ax1.set_title(lc['ImageName'][k], fontsize=14)
# plot right column
ax2.imshow(im2, origin="upper", cmap="gray")
xbox = np.array([-1, 1])*imsize1/2 + (imsize2-1)//2
ax2.plot(xbox[[0, 1, 1, 0, 0]], xbox[[0, 0, 1, 1, 0]], 'r-', linewidth=1)
ax2.set_title(f"m={lc['CorrMag'][k]:.3f} MJD={lc['MJD'][k]:.2f}", fontsize=14)
print(f"{(time.time()-t0):.1f} s: finished {i} of {len(ind)} epochs")
print(f"{(time.time()-t0):.1f} s: got {nrows*ncols} cutouts")
1.7 s: finished 1 of 5 epochs
3.4 s: finished 2 of 5 epochs
5.0 s: finished 3 of 5 epochs
6.5 s: finished 4 of 5 epochs
8.1 s: finished 5 of 5 epochs
8.1 s: got 10 cutouts