Flux Unit Conversions with synphot and stsynphot#
Learning Goals#
By the end of this tutorial, you will:
Perform conversions between various systems of flux and magnitude using the
synphotandstsynphotpackages.Extrapolate an output flux at a different wavelength than the input flux, by using a spectrum defined using the same packages.
Provide a framework to adapt a more personalized and streamlined conversion process, if desired.
Table of Contents#
Introduction
1. Imports
2. Input and output setup
2.1 Units
2.2 Bandpasses
2.3 Choosing a spectrum
2.4 User settings
3. Set up the conversion
4. Perform the conversion and create a plot
5. Examples
5.1 Flux in Jy to AB mag with a flat spectrum in \(F_\nu\)
5.2 Flux in flam to Flux in flam along a blackbody
5.3 Flux in fnu to flux in photnu, any spectrum (same wavelength)
5.4 mag to mag from an HST bandpass to a Johnson bandpass, flat spectrum in \(F_\lambda\)
6. Conclusions
Additional Resources
About the Notebook
Citations
Introduction#
This notebook is based on the prior “HST Photometric Conversion Tool” that returns unit conversions between various flux units and magnitude systems. It is not intended to replace more detailed functionality such as that provided by the Exposure Time Calculator (ETC). Rather, it is intended to provide a simple, quick result for flux unit conversions.
stsynphot requires access to data distributed by the Calibration Data Reference System (CRDS) in order to operate. Both packages look for an environment variable called PYSYN_CDBS to find the directory containing these data.
Users can obtain these data files from the CDRS. Information on how to obtain the most up-to-date reference files (and what they contain) can be found here. An example of how to download these files using curl and set up this environment variable is presented in the imports section below.
For detailed instructions on how to install and set up these packages, see the synphot and stsynphot documentation.
1. Imports#
This notebook assumes you have created the virtual environment in WFC3 notebooks’ installation instructions.
We import:
os for setting environment variables
tarfile for extracting a .tar archive
numpy for handling array functions
matplotlib.pyplot for plotting data
synphot and stsynphot for evaluating synthetic photometry
astropy.units and synphot.units for handling units
Additionally, we will need to set the PYSYN_CDBS environment variable before importing stsynphot. We will also create a Vega spectrum using synphot’s inbuilt from_vega() method, as the latter package will supercede this method’s functionality and require a downloaded copy of the latest Vega spectrum to be provided.
import os
import tarfile
import numpy as np
import matplotlib.pyplot as plt
from synphot import SourceSpectrum
from synphot.models import BlackBody1D, PowerLawFlux1D
from synphot.units import convert_flux
from astropy import units as u
from synphot import units as su
%matplotlib inline
vegaspec = SourceSpectrum.from_vega()
This section obtains the WFC3 throughput component tables for use with stsynphot. This step only needs to be done once. If these reference files have already been downloaded, this section can be skipped.
!curl -O https://archive.stsci.edu/hlsps/reference-atlases/hlsp_reference-atlases_hst_multi_everything_multi_v11_sed.tar
% Total % Received % Xferd Average Speed Time Time Time Current
Dload Upload Total Spent Left Speed
0 0 0 0 0 0 0 0 --:--:-- --:--:-- --:--:-- 0
0 0 0 0 0 0 0 0 --:--:-- --:--:-- --:--:-- 0
0 796M 0 2448k 0 0 2275k 0 0:05:58 0:00:01 0:05:57 2275k
0 796M 0 5952k 0 0 2946k 0 0:04:36 0:00:02 0:04:34 2946k
0 796M 0 7648k 0 0 2517k 0 0:05:23 0:00:03 0:05:20 2516k
1 796M 1 8768k 0 0 2148k 0 0:06:19 0:00:04 0:06:15 2147k
1 796M 1 9728k 0 0 1935k 0 0:07:01 0:00:05 0:06:56 1943k
1 796M 1 10.5M 0 0 1793k 0 0:07:34 0:00:06 0:07:28 1688k
1 796M 1 11.3M 0 0 1654k 0 0:08:12 0:00:07 0:08:05 1133k
1 796M 1 12.0M 0 0 1541k 0 0:08:48 0:00:08 0:08:40 947k
1 796M 1 12.8M 0 0 1461k 0 0:09:17 0:00:09 0:09:08 895k
1 796M 1 13.5M 0 0 1376k 0 0:09:52 0:00:10 0:09:42 816k
1 796M 1 14.1M 0 0 1313k 0 0:10:20 0:00:11 0:10:09 738k
1 796M 1 14.9M 0 0 1271k 0 0:10:41 0:00:12 0:10:29 736k
1 796M 1 15.5M 0 0 1225k 0 0:11:05 0:00:13 0:10:52 715k
2 796M 2 16.2M 0 0 1184k 0 0:11:28 0:00:14 0:11:14 684k
2 796M 2 16.9M 0 0 1153k 0 0:11:47 0:00:15 0:11:32 704k
2 796M 2 17.6M 0 0 1128k 0 0:12:02 0:00:16 0:11:46 717k
2 796M 2 18.5M 0 0 1113k 0 0:12:12 0:00:17 0:11:55 733k
2 796M 2 19.5M 0 0 1108k 0 0:12:15 0:00:18 0:11:57 809k
2 796M 2 20.2M 0 0 1089k 0 0:12:28 0:00:19 0:12:09 820k
2 796M 2 20.7M 0 0 1063k 0 0:12:46 0:00:20 0:12:26 793k
2 796M 2 21.5M 0 0 1047k 0 0:12:58 0:00:21 0:12:37 785k
2 796M 2 22.2M 0 0 1033k 0 0:13:08 0:00:22 0:12:46 759k
2 796M 2 22.6M 0 0 1007k 0 0:13:29 0:00:23 0:13:06 638k
2 796M 2 23.2M 0 0 989k 0 0:13:44 0:00:24 0:13:20 611k
2 796M 2 23.7M 0 0 972k 0 0:13:58 0:00:25 0:13:33 607k
3 796M 3 24.3M 0 0 956k 0 0:14:12 0:00:26 0:13:46 575k
3 796M 3 24.9M 0 0 943k 0 0:14:24 0:00:27 0:13:57 543k
3 796M 3 25.5M 0 0 934k 0 0:14:32 0:00:28 0:14:04 596k
3 796M 3 26.1M 0 0 922k 0 0:14:43 0:00:29 0:14:14 600k
3 796M 3 26.6M 0 0 908k 0 0:14:57 0:00:30 0:14:27 589k
3 796M 3 27.0M 0 0 892k 0 0:15:13 0:00:31 0:14:42 561k
3 796M 3 27.5M 0 0 880k 0 0:15:25 0:00:32 0:14:53 542k
3 796M 3 28.0M 0 0 868k 0 0:15:38 0:00:33 0:15:05 498k
3 796M 3 28.5M 0 0 857k 0 0:15:51 0:00:34 0:15:17 478k
3 796M 3 29.0M 0 0 850k 0 0:15:59 0:00:35 0:15:24 496k
3 796M 3 29.6M 0 0 843k 0 0:16:06 0:00:36 0:15:30 538k
3 796M 3 30.3M 0 0 839k 0 0:16:10 0:00:37 0:15:33 578k
3 796M 3 31.2M 0 0 841k 0 0:16:09 0:00:38 0:15:31 661k
4 796M 4 32.2M 0 0 845k 0 0:16:04 0:00:39 0:15:25 764k
4 796M 4 33.0M 0 0 846k 0 0:16:03 0:00:40 0:15:23 822k
4 796M 4 34.1M 0 0 851k 0 0:15:57 0:00:41 0:15:16 909k
4 796M 4 35.2M 0 0 858k 0 0:15:49 0:00:42 0:15:07 998k
4 796M 4 36.5M 0 0 869k 0 0:15:37 0:00:43 0:14:54 1088k
4 796M 4 37.5M 0 0 873k 0 0:15:32 0:00:44 0:14:48 1096k
4 796M 4 38.3M 0 0 871k 0 0:15:35 0:00:45 0:14:50 1068k
4 796M 4 38.8M 0 0 864k 0 0:15:42 0:00:46 0:14:56 974k
4 796M 4 39.5M 0 0 861k 0 0:15:46 0:00:47 0:14:59 881k
5 796M 5 40.4M 0 0 860k 0 0:15:47 0:00:48 0:14:59 786k
5 796M 5 41.4M 0 0 863k 0 0:15:43 0:00:49 0:14:54 776k
5 796M 5 42.4M 0 0 869k 0 0:15:37 0:00:50 0:14:47 852k
5 796M 5 43.4M 0 0 871k 0 0:15:35 0:00:51 0:14:44 937k
5 796M 5 44.5M 0 0 877k 0 0:15:29 0:00:52 0:14:37 1032k
5 796M 5 45.7M 0 0 881k 0 0:15:24 0:00:53 0:14:31 1082k
5 796M 5 46.6M 0 0 883k 0 0:15:23 0:00:54 0:14:29 1075k
5 796M 5 47.4M 0 0 882k 0 0:15:23 0:00:55 0:14:28 1012k
6 796M 6 48.1M 0 0 878k 0 0:15:27 0:00:56 0:14:31 949k
6 796M 6 48.8M 0 0 877k 0 0:15:29 0:00:57 0:14:32 877k
6 796M 6 49.6M 0 0 875k 0 0:15:31 0:00:58 0:14:33 808k
6 796M 6 50.4M 0 0 874k 0 0:15:32 0:00:59 0:14:33 782k
6 796M 6 51.1M 0 0 872k 0 0:15:34 0:01:00 0:14:34 762k
6 796M 6 51.9M 0 0 871k 0 0:15:35 0:01:01 0:14:34 789k
6 796M 6 52.7M 0 0 871k 0 0:15:35 0:01:02 0:14:33 804k
6 796M 6 53.7M 0 0 873k 0 0:15:33 0:01:03 0:14:30 854k
6 796M 6 54.7M 0 0 876k 0 0:15:30 0:01:04 0:14:26 896k
6 796M 6 55.4M 0 0 873k 0 0:15:33 0:01:05 0:14:28 884k
7 796M 7 56.0M 0 0 869k 0 0:15:37 0:01:06 0:14:31 842k
7 796M 7 56.7M 0 0 867k 0 0:15:39 0:01:07 0:14:32 819k
7 796M 7 57.6M 0 0 867k 0 0:15:39 0:01:08 0:14:31 793k
7 796M 7 58.4M 0 0 867k 0 0:15:39 0:01:09 0:14:30 753k
7 796M 7 59.1M 0 0 864k 0 0:15:43 0:01:10 0:14:33 743k
7 796M 7 59.6M 0 0 860k 0 0:15:47 0:01:11 0:14:36 735k
7 796M 7 60.2M 0 0 856k 0 0:15:51 0:01:12 0:14:39 711k
7 796M 7 60.9M 0 0 853k 0 0:15:54 0:01:13 0:14:41 663k
7 796M 7 61.6M 0 0 852k 0 0:15:56 0:01:14 0:14:42 642k
7 796M 7 62.4M 0 0 851k 0 0:15:56 0:01:15 0:14:41 681k
7 796M 7 63.2M 0 0 852k 0 0:15:56 0:01:16 0:14:40 738k
8 796M 8 64.1M 0 0 851k 0 0:15:57 0:01:17 0:14:40 781k
8 796M 8 65.0M 0 0 853k 0 0:15:55 0:01:18 0:14:37 839k
8 796M 8 65.9M 0 0 854k 0 0:15:54 0:01:19 0:14:35 885k
8 796M 8 66.5M 0 0 851k 0 0:15:57 0:01:20 0:14:37 843k
8 796M 8 67.0M 0 0 847k 0 0:16:01 0:01:21 0:14:40 781k
8 796M 8 67.7M 0 0 845k 0 0:16:03 0:01:22 0:14:41 750k
8 796M 8 68.5M 0 0 845k 0 0:16:04 0:01:23 0:14:41 726k
8 796M 8 69.4M 0 0 846k 0 0:16:02 0:01:24 0:14:38 729k
8 796M 8 70.5M 0 0 849k 0 0:15:59 0:01:25 0:14:34 823k
9 796M 9 71.7M 0 0 854k 0 0:15:54 0:01:26 0:14:28 957k
9 796M 9 72.7M 0 0 856k 0 0:15:51 0:01:27 0:14:24 1033k
9 796M 9 73.5M 0 0 855k 0 0:15:52 0:01:28 0:14:24 1026k
9 796M 9 74.2M 0 0 854k 0 0:15:54 0:01:29 0:14:25 975k
9 796M 9 75.0M 0 0 853k 0 0:15:54 0:01:30 0:14:24 924k
9 796M 9 76.0M 0 0 855k 0 0:15:53 0:01:31 0:14:22 873k
9 796M 9 76.8M 0 0 855k 0 0:15:52 0:01:32 0:14:20 839k
9 796M 9 77.7M 0 0 856k 0 0:15:52 0:01:33 0:14:19 863k
9 796M 9 78.5M 0 0 855k 0 0:15:53 0:01:34 0:14:19 877k
9 796M 9 79.2M 0 0 853k 0 0:15:55 0:01:35 0:14:20 845k
10 796M 10 79.9M 0 0 852k 0 0:15:56 0:01:36 0:14:20 801k
10 796M 10 80.4M 0 0 849k 0 0:16:00 0:01:37 0:14:23 728k
10 796M 10 81.0M 0 0 846k 0 0:16:03 0:01:38 0:14:25 661k
10 796M 10 81.6M 0 0 844k 0 0:16:05 0:01:39 0:14:26 635k
10 796M 10 82.2M 0 0 842k 0 0:16:07 0:01:40 0:14:27 630k
10 796M 10 82.9M 0 0 840k 0 0:16:10 0:01:41 0:14:29 607k
10 796M 10 83.4M 0 0 837k 0 0:16:13 0:01:42 0:14:31 618k
10 796M 10 83.9M 0 0 834k 0 0:16:17 0:01:43 0:14:34 596k
10 796M 10 84.4M 0 0 831k 0 0:16:20 0:01:44 0:14:36 578k
10 796M 10 85.1M 0 0 830k 0 0:16:22 0:01:45 0:14:37 586k
10 796M 10 85.8M 0 0 829k 0 0:16:23 0:01:46 0:14:37 602k
10 796M 10 86.5M 0 0 828k 0 0:16:24 0:01:47 0:14:37 633k
10 796M 10 87.3M 0 0 828k 0 0:16:24 0:01:48 0:14:36 705k
11 796M 11 88.2M 0 0 828k 0 0:16:23 0:01:49 0:14:34 769k
11 796M 11 88.8M 0 0 826k 0 0:16:26 0:01:50 0:14:36 753k
11 796M 11 89.3M 0 0 823k 0 0:16:29 0:01:51 0:14:38 712k
11 796M 11 89.9M 0 0 822k 0 0:16:31 0:01:52 0:14:39 693k
11 796M 11 90.7M 0 0 821k 0 0:16:32 0:01:53 0:14:39 680k
11 796M 11 91.4M 0 0 820k 0 0:16:33 0:01:54 0:14:39 650k
11 796M 11 92.0M 0 0 819k 0 0:16:34 0:01:55 0:14:39 662k
11 796M 11 92.7M 0 0 818k 0 0:16:35 0:01:56 0:14:39 703k
11 796M 11 93.5M 0 0 818k 0 0:16:35 0:01:57 0:14:38 743k
11 796M 11 94.5M 0 0 820k 0 0:16:34 0:01:58 0:14:36 786k
11 796M 11 95.4M 0 0 821k 0 0:16:32 0:01:59 0:14:33 828k
12 796M 12 96.4M 0 0 822k 0 0:16:31 0:02:00 0:14:31 894k
12 796M 12 97.4M 0 0 824k 0 0:16:28 0:02:01 0:14:27 965k
12 796M 12 98.3M 0 0 825k 0 0:16:27 0:02:02 0:14:25 984k
12 796M 12 99.2M 0 0 826k 0 0:16:26 0:02:03 0:14:23 977k
12 796M 12 100M 0 0 826k 0 0:16:26 0:02:04 0:14:22 960k
12 796M 12 101M 0 0 827k 0 0:16:25 0:02:05 0:14:20 940k
12 796M 12 101M 0 0 826k 0 0:16:25 0:02:06 0:14:19 881k
12 796M 12 102M 0 0 825k 0 0:16:27 0:02:07 0:14:20 819k
12 796M 12 103M 0 0 824k 0 0:16:29 0:02:08 0:14:21 767k
13 796M 13 103M 0 0 823k 0 0:16:30 0:02:09 0:14:21 740k
13 796M 13 104M 0 0 822k 0 0:16:31 0:02:10 0:14:21 690k
13 796M 13 105M 0 0 821k 0 0:16:32 0:02:11 0:14:21 686k
13 796M 13 105M 0 0 819k 0 0:16:34 0:02:12 0:14:22 671k
13 796M 13 106M 0 0
817k 0 0:16:37 0:02:13 0:14:24 646k
13 796M 13 106M 0 0 816k 0 0:16:38 0:02:14 0:14:24 645k
13 796M 13 107M 0 0 814k 0 0:16:40 0:02:15 0:14:25 626k
13 796M 13 107M 0 0 812k 0 0:16:44 0:02:16 0:14:28 561k
13 796M 13 108M 0 0 809k 0 0:16:46 0:02:17 0:14:29 550k
13 796M 13 108M 0 0 808k 0 0:16:48 0:02:18 0:14:30 562k
13 796M 13 109M 0 0 808k 0 0:16:48 0:02:19 0:14:29 574k
13 796M 13 110M 0 0 807k 0 0:16:49 0:02:20 0:14:29 613k
13 796M 13 111M 0 0 807k 0 0:16:49 0:02:21 0:14:28 688k
14 796M 14 112M 0 0 808k 0 0:16:48 0:02:22 0:14:26 771k
14 796M 14 113M 0 0 809k 0 0:16:47 0:02:23 0:14:24 836k
14 796M 14 113M 0 0 809k 0 0:16:46 0:02:24 0:14:22 855k
14 796M 14 114M 0 0 811k 0 0:16:45 0:02:25 0:14:20 905k
14 796M 14 115M 0 0 812k 0 0:16:42 0:02:26 0:14:16 959k
14 796M 14 117M 0 0 815k 0 0:16:39 0:02:27 0:14:12 1014k
14 796M 14 118M 0 0 818k 0 0:16:36 0:02:28 0:14:08 1087k
15 796M 15 119M 0 0 822k 0 0:16:30 0:02:29 0:14:01 1202k
15 796M 15 121M 0 0 826k 0 0:16:25 0:02:30 0:13:55 1282k
15 796M 15 122M 0 0 830k 0 0:16:22 0:02:31 0:13:51 1338k
15 796M 15 123M 0 0 834k 0 0:16:17 0:02:32 0:13:45 1382k
15 796M 15 125M 0 0 836k 0 0:16:14 0:02:33 0:13:41 1355k
15 796M 15 125M 0 0 836k 0 0:16:15 0:02:34 0:13:41 1233k
15 796M 15 126M 0 0 834k 0 0:16:16 0:02:35 0:13:41 1064k
15 796M 15 127M 0 0 833k 0 0:16:17 0:02:36 0:13:41 942k
16 796M 16 127M 0 0 833k 0 0:16:18 0:02:37 0:13:41 807k
16 796M 16 128M 0 0 831k 0 0:16:20 0:02:38 0:13:42 696k
16 796M 16 128M 0 0 829k 0 0:16:22 0:02:39 0:13:43 635k
16 796M 16 129M 0 0 828k 0 0:16:24 0:02:40 0:13:44 630k
16 796M 16 130M 0 0 827k 0 0:16:25 0:02:41 0:13:44 628k
16 796M 16 130M 0 0 827k 0 0:16:25 0:02:42 0:13:43 643k
16 796M 16 131M 0 0 828k 0 0:16:24 0:02:43 0:13:41 713k
16 796M 16 132M 0 0 829k 0 0:16:22 0:02:44 0:13:38 827k
16 796M 16 133M 0 0 830k 0 0:16:21 0:02:45 0:13:36 911k
16 796M 16 134M 0 0 832k 0 0:16:19 0:02:46 0:13:33 988k
17 796M 17 136M 0 0 834k 0 0:16:17 0:02:47 0:13:30 1060k
17 796M 17 137M 0 0 836k 0 0:16:15 0:02:48 0:13:27 1091k
17 796M 17 138M 0 0 837k 0 0:16:13 0:02:49 0:13:24 1084k
17 796M 17 139M 0 0 839k 0 0:16:10 0:02:50 0:13:20 1143k
17 796M 17 140M 0 0 841k 0 0:16:08 0:02:51 0:13:17 1160k
17 796M 17 141M 0 0 841k 0 0:16:08 0:02:52 0:13:16 1074k
17 796M 17 141M 0 0 840k 0 0:16:10 0:02:53 0:13:17 981k
17 796M 17 142M 0 0 839k 0 0:16:11 0:02:54 0:13:17 896k
17 796M 17 143M 0 0 837k 0 0:16:14 0:02:55 0:13:19 741k
18 796M 18 143M 0 0 835k 0 0:16:15 0:02:56 0:13:19 632k
18 796M 18 144M 0 0 835k 0 0:16:16 0:02:57 0:13:19 622k
18 796M 18 145M 0 0 835k 0 0:16:16 0:02:58 0:13:18 665k
18 796M 18 145M 0 0 834k 0 0:16:17 0:02:59 0:13:18 661k
18 796M 18 146M 0 0 833k 0 0:16:18 0:03:00 0:13:18 697k
18 796M 18 147M 0 0 832k 0 0:16:18 0:03:01 0:13:17 724k
18 796M 18 148M 0 0 833k 0 0:16:18 0:03:02 0:13:16 757k
18 796M 18 148M 0 0 832k 0 0:16:18 0:03:03 0:13:15 749k
18 796M 18 149M 0 0 831k 0 0:16:19 0:03:04 0:13:15 757k
18 796M 18 150M 0 0 831k 0 0:16:20 0:03:05 0:13:15 780k
18 796M 18 150M 0 0 830k 0 0:16:21 0:03:06 0:13:15 740k
19 796M 19 151M 0 0 828k 0 0:16:24 0:03:07 0:13:17 647k
19 796M 19 151M 0 0 826k 0 0:16:26 0:03:08 0:13:18 597k
19 796M 19 152M 0 0 825k 0 0:16:27 0:03:09 0:13:18 598k
19 796M 19 153M 0 0 825k 0 0:16:27 0:03:10 0:13:17 595k
19 796M 19 153M 0 0 825k 0 0:16:28 0:03:11 0:13:17 629k
19 796M 19 154M 0 0 824k 0 0:16:28 0:03:12 0:13:16 705k
19 796M 19 155M 0 0 825k 0 0:16:27 0:03:13 0:13:14 781k
19 796M 19 156M 0 0 826k 0 0:16:26 0:03:14 0:13:12 865k
19 796M 19 157M 0 0 827k 0 0:16:24 0:03:15 0:13:09 912k
19 796M 19 158M 0 0 827k 0 0:16:24 0:03:16 0:13:08 933k
19 796M 19 159M 0 0 827k 0 0:16:25 0:03:17 0:13:08 907k
20 796M 20 159M 0 0 826k 0 0:16:26 0:03:18 0:13:08 867k
20 796M 20 160M 0 0 825k 0 0:16:27 0:03:19 0:13:08 791k
20 796M 20 161M 0 0 825k 0 0:16:27 0:03:20 0:13:07 744k
20 796M 20 162M 0 0 825k 0 0:16:27 0:03:21 0:13:06 749k
20 796M 20 163M 0 0 826k 0 0:16:26 0:03:22 0:13:04 810k
20 796M 20 163M 0 0 826k 0 0:16:26 0:03:23 0:13:03 808k
20 796M 20 164M 0 0 825k 0 0:16:27 0:03:24 0:13:03 813k
20 796M 20 165M 0 0 825k 0 0:16:27 0:03:25 0:13:02 831k
20 796M 20 166M 0 0 825k 0 0:16:27 0:03:26 0:13:01 807k
20 796M 20 166M 0 0 825k 0 0:16:27 0:03:27 0:13:00 789k
21 796M 21 167M 0 0 826k 0 0:16:26 0:03:28 0:12:58 837k
21 796M 21 168M 0 0 827k 0 0:16:25 0:03:29 0:12:56 910k
21 796M 21 170M 0 0 829k 0 0:16:23 0:03:30 0:12:53 972k
21 796M 21 171M 0 0 830k 0 0:16:21 0:03:31 0:12:50 1034k
21 796M 21 172M 0 0 831k 0 0:16:20 0:03:32 0:12:48 1072k
21 796M 21 173M 0 0 832k 0 0:16:19 0:03:33 0:12:46 1077k
21 796M 21 174M 0 0 833k 0 0:16:18 0:03:34 0:12:44 1066k
21 796M 21 175M 0 0 833k 0 0:16:17 0:03:35 0:12:42 1030k
22 796M 22 176M 0 0 835k 0 0:16:16 0:03:36 0:12:40 1038k
22 796M 22 177M 0 0 836k 0 0:16:14 0:03:37 0:12:37 1060k
22 796M 22 178M 0 0 838k 0 0:16:12 0:03:38 0:12:34 1096k
22 796M 22 179M 0 0 838k 0 0:16:12 0:03:39 0:12:33 1049k
22 796M 22 179M 0 0 837k 0 0:16:13 0:03:40 0:12:33 988k
22 796M 22 180M 0 0 836k 0 0:16:14 0:03:41 0:12:33 897k
22 796M 22 181M 0 0 835k 0 0:16:15 0:03:42 0:12:33 789k
22 796M 22 181M 0 0 834k 0 0:16:16 0:03:43 0:12:33 685k
22 796M 22 182M 0 0 834k 0 0:16:17 0:03:44 0:12:33 667k
23 796M 23 183M 0 0 834k 0 0:16:17 0:03:45 0:12:32 694k
23 796M 23 184M 0 0 834k 0 0:16:16 0:03:46 0:12:30 749k
23 796M 23 185M 0 0 835k 0 0:16:15 0:03:47 0:12:28 838k
23 796M 23 186M 0 0 837k 0 0:16:13 0:03:48 0:12:25 954k
23 796M 23 187M 0 0 839k 0 0:16:11 0:03:49 0:12:22 1053k
23 796M 23 188M 0 0 839k 0 0:16:11 0:03:50 0:12:21 1062k
23 796M 23 189M 0 0 839k 0 0:16:10 0:03:51 0:12:19 1066k
23 796M 23 190M 0 0 840k 0 0:16:09 0:03:52 0:12:17 1055k
24 796M 24 191M 0 0 842k 0 0:16:08 0:03:53 0:12:15 1054k
24 796M 24 192M 0 0 844k 0 0:16:05 0:03:54 0:12:11 1079k
24 796M 24 194M 0 0 846k 0 0:16:02 0:03:55 0:12:07 1200k
24 796M 24 195M 0 0 850k 0 0:15:59 0:03:56 0:12:03 1329k
24 796M 24 197M 0 0 853k 0 0:15:55 0:03:57 0:11:58 1452k
24 796M 24 199M 0 0 856k 0 0:15:52 0:03:58 0:11:54 1498k
25 796M 25 200M 0 0 858k 0 0:15:49 0:03:59 0:11:50 1510k
25 796M 25 201M 0 0 860k 0 0:15:47 0:04:00 0:11:47 1483k
25 796M 25 202M 0 0 861k 0 0:15:46 0:04:01 0:11:45 1378k
25 796M 25 203M 0 0 861k 0 0:15:46 0:04:02 0:11:44 1223k
25 796M 25 204M 0 0 860k 0 0:15:47 0:04:03 0:11:44 1050k
25 796M 25 204M 0 0 859k 0 0:15:49 0:04:04 0:11:45 895k
25 796M 25 205M 0 0 858k 0 0:15:49 0:04:05 0:11:44 773k
25 796M 25 206M 0 0 858k 0 0:15:49 0:04:06 0:11:43 727k
26 796M 26 207M 0 0 858k 0 0:15:49 0:04:07 0:11:42 753k
26 796M 26 208M 0 0 859k 0 0:15:48 0:04:08 0:11:40 856k
26 796M 26 209M 0 0 860k 0 0:15:47 0:04:09 0:11:38 950k
26 796M 26 210M 0 0 860k 0 0:15:47 0:04:10 0:11:37 948k
26 796M 26 210M 0 0 860k 0 0:15:47 0:04:11 0:11:36 947k
26 796M 26 211M 0 0 860k 0 0:15:47 0:04:12 0:11:35 945k
26 796M 26 212M 0 0 861k 0 0:15:46 0:04:13 0:11:33 918k
26 796M 26 213M 0 0 860k 0 0:15:47 0:04:14 0:11:33 838k
26 796M 26 214M 0 0 860k 0 0:15:47 0:04:15 0:11:32 854k
26 796M 26 214M 0 0 858k 0 0:15:49 0:04:16 0:11:33 776k
27 796M 27 215M 0 0 856k 0 0:15:51 0:04:17 0:11:34 669k
27 796M 27 215M 0 0 855k 0 0:15:52 0:04:18 0:11:34 588k
27 796M 27 216M 0 0 855k 0 0:15:53 0:04:19 0:11:34 581k
27 796M 27 217M 0 0 854k 0 0:15:53 0:04:20 0:11:33 584k
27 796M 27 217M 0 0 854k 0 0:15:54 0:04:21 0:11:33 634k
27 796M 27 218M 0 0 854k 0 0:15:54 0:04:22 0:11:32 715k
27 796M 27 219M 0 0 854k 0 0:15:54 0:04:23 0:11:31 785k
27 796M 27 220M 0 0 855k 0 0:15:53 0:04:24 0:11:29 872k
27 796M 27 221M 0 0 856k 0 0:15:51 0:04:25 0:11:26 948k
28 796M 28 222M 0 0 858k 0 0:15:49 0:04:26 0:11:23 1074k
28 796M 28 224M 0 0 859k 0 0:15:48 0:04:27 0:11:21 1141k
28 796M 28 225M 0 0 861k 0 0:15:46 0:04:28 0:11:18 1210k
28 796M 28 226M 0 0 862k 0 0:15:45 0:04:29 0:11:16 1246k
28 796M 28 227M 0 0 862k 0 0:15:44 0:04:30 0:11:14 1188k
28 796M 28 228M 0 0 862k 0 0:15:44 0:04:31 0:11:13 1105k
28 796M 28 229M 0 0 863k 0 0:15:44 0:04:32 0:11:12 1070k
28 796M 28 230M 0 0 864k 0 0:15:43 0:04:33 0:11:10 1042k
29 796M 29 231M 0 0 866k 0 0:15:41 0:04:34 0:11:07 1050k
29 796M 29 233M 0 0 868k 0 0:15:39 0:04:35 0:11:04 1153k
29 796M 29 234M 0 0 870k 0 0:15:36 0:04:36 0:11:00 1285k
29 796M 29 236M 0 0 872k 0 0:15:34 0:04:37 0:10:57 1362k
29 796M 29 237M 0 0 874k 0 0:15:32 0:04:38 0:10:54 1433k
30 796M 30 239M 0 0 877k 0 0:15:29 0:04:39 0:10:50 1484k
30 796M 30 240M 0 0 877k 0 0:15:29 0:04:40 0:10:49 1398k
30 796M 30 240M 0 0 877k 0 0:15:28 0:04:41 0:10:47 1289k
30 796M 30 241M 0 0 877k 0 0:15:29 0:04:42 0:10:47 1142k
30 796M 30 242M 0 0 876k 0 0:15:30 0:04:43 0:10:47 965k
30 796M 30 242M 0 0 875k 0 0:15:31 0:04:44 0:10:47 787k
30 796M 30 243M 0 0 875k 0 0:15:31 0:04:45 0:10:46 739k
30 796M 30 244M 0 0 874k 0 0:15:32 0:04:46 0:10:46 665k
30 796M 30 244M 0 0 873k 0 0:15:33 0:04:47 0:10:46 645k
30 796M 30 245M 0 0 872k 0 0:15:34 0:04:48 0:10:46 664k
30 796M 30 246M 0 0 872k 0 0:15:34 0:04:49 0:10:45 696k
31 796M 31 247M 0 0 872k 0 0:15:34 0:04:50 0:10:44 699k
31 796M 31 247M 0 0 872k 0 0:15:34 0:04:51 0:10:43 747k
31 796M 31 248M 0 0 872k 0 0:15:34 0:04:52 0:10:42 828k
31 796M 31 249M 0 0 873k 0 0:15:33 0:04:53 0:10:40 901k
31 796M 31 251M 0 0 874k 0 0:15:32 0:04:54 0:10:38 975k
31 796M 31 252M 0 0 875k 0 0:15:30 0:04:55 0:10:35 1093k
31 796M 31 253M 0 0 877k 0 0:15:28 0:04:56 0:10:32 1218k
32 796M 32 255M 0 0 879k 0 0:15:26 0:04:57 0:10:29 1321k
32 796M 32 256M 0 0 881k 0 0:15:24 0:04:58 0:10:26 1373k
32 796M 32 258M 0 0 883k 0 0:15:22 0:04:59 0:10:23 1450k
32 796M 32 259M 0 0 886k 0 0:15:19 0:05:00 0:10:19 1500k
32 796M 32 261M 0 0 888k 0 0:15:17 0:05:01 0:10:16 1530k
33 796M 33 263M 0 0 891k 0 0:15:14 0:05:02 0:10:12 1590k
33 796M 33 264M 0 0 894k 0 0:15:11 0:05:03 0:10:08 1671k
33 796M 33 265M 0 0 895k 0 0:15:10 0:05:04 0:10:06 1570k
33 796M 33 266M 0 0 895k 0 0:15:10 0:05:05 0:10:05 1454k
33 796M 33 267M 0 0 895k 0 0:15:10 0:05:06 0:10:04 1326k
33 796M 33 268M 0 0 896k 0 0:15:09 0:05:07 0:10:02 1195k
33 796M 33 270M 0 0 897k 0 0:15:08 0:05:08 0:10:00 1084k
34 796M 34 271M 0 0 898k 0 0:15:07 0:05:09 0:09:58 1080k
34 796M 34 272M 0 0 898k 0 0:15:07 0:05:10 0:09:57 1087k
34 796M 34 273M 0 0 898k 0 0:15:07 0:05:11 0:09:56 1073k
34 796M 34 273M 0 0 898k 0 0:15:07 0:05:12 0:09:55 1022k
34 796M 34 274M 0 0 898k 0 0:15:07 0:05:13 0:09:54 970k
34 796M 34 275M 0 0 898k 0 0:15:07 0:05:14 0:09:53 921k
34 796M 34 276M 0 0 898k 0 0:15:07 0:05:15 0:09:52 871k
34 796M 34 277M 0 0 897k 0 0:15:08 0:05:16 0:09:52 842k
34 796M 34 277M 0 0 897k 0 0:15:08 0:05:17 0:09:51 839k
35 796M 35 278M 0 0 897k 0 0:15:07 0:05:18 0:09:49 846k
35 796M 35 279M 0 0 897k 0 0:15:08 0:05:19 0:09:49 861k
35 796M 35 280M 0 0 898k 0 0:15:07 0:05:20 0:09:47 898k
35 796M 35 281M 0 0 898k 0 0:15:07 0:05:21 0:09:46 953k
35 796M 35 282M 0 0 899k 0 0:15:06 0:05:22 0:09:44 1006k
35 796M 35 283M 0 0 899k 0 0:15:06 0:05:23 0:09:43 986k
35 796M 35 284M 0 0 899k 0 0:15:06 0:05:24 0:09:42 985k
35 796M 35 285M 0 0 899k 0 0:15:06 0:05:25 0:09:41 979k
35 796M 35 286M 0 0 900k 0 0:15:05 0:05:26 0:09:39 994k
36 796M 36 287M 0 0 901k 0 0:15:04 0:05:27 0:09:37 1024k
36 796M 36 289M 0 0 902k 0 0:15:03 0:05:28 0:09:35 1124k
36 796M 36 290M 0 0 902k 0 0:15:02 0:05:29 0:09:33 1143k
36 796M 36 290M 0 0 902k 0 0:15:03 0:05:30 0:09:33 1085k
36 796M 36 291M 0 0 901k 0 0:15:04 0:05:31 0:09:33 972k
36 796M 36 291M 0 0 900k 0 0:15:05 0:05:32 0:09:33 836k
36 796M 36 292M 0 0 899k 0 0:15:06 0:05:33 0:09:33 683k
36 796M 36 293M 0 0 898k 0 0:15:06 0:05:34 0:09:32 633k
36 796M 36 294M 0 0 898k 0 0:15:07 0:05:35 0:09:32 672k
37 796M 37 295M 0 0 898k 0 0:15:07 0:05:36 0:09:31 742k
37 796M 37 295M 0 0 898k 0 0:15:06 0:05:37 0:09:29 805k
37 796M 37 296M 0 0 899k 0 0:15:06 0:05:38 0:09:28 877k
37 796M 37 297M 0 0 899k 0 0:15:06 0:05:39 0:09:27 900k
37 796M 37 298M 0 0 898k 0 0:15:07 0:05:40 0:09:27 861k
37 796M 37 298M 0 0 897k 0 0:15:08 0:05:41 0:09:27 804k
37 796M 37 299M 0 0 897k 0 0:15:08 0:05:42 0:09:26 770k
37 796M 37 300M 0 0 896k 0 0:15:09 0:05:43 0:09:26 735k
37 796M 37 301M 0 0 896k 0 0:15:08 0:05:44 0:09:24 759k
37 796M 37 302M 0 0 897k 0 0:15:08 0:05:45 0:09:23 847k
38 796M 38 303M 0 0 898k 0 0:15:07 0:05:46 0:09:21 966k
38 796M 38 304M 0 0 899k 0 0:15:06 0:05:47 0:09:19 1092k
38 796M 38 306M 0 0 901k 0 0:15:04 0:05:48 0:09:16 1226k
38 796M 38 307M 0 0 903k 0 0:15:02 0:05:49 0:09:13 1343k
38 796M 38 309M 0 0 904k 0 0:15:01 0:05:50 0:09:11 1382k
38 796M 38 310M 0 0 905k 0 0:15:00 0:05:51 0:09:09 1376k
39 796M 39 311M 0 0 905k 0 0:15:00 0:05:52 0:09:08 1295k
39 796M 39 312M 0 0 906k 0 0:14:59 0:05:53 0:09:06 1216k
39 796M 39 313M 0 0 906k 0 0:14:59 0:05:54 0:09:05 1090k
39 796M 39 313M 0 0 904k 0 0:15:01 0:05:55 0:09:06 932k
39 796M 39 314M 0 0 903k 0 0:15:02 0:05:56 0:09:06 780k
39 796M 39 314M 0 0 902k 0 0:15:03 0:05:57 0:09:06 669k
39 796M 39 315M 0 0 901k 0 0:15:04 0:05:58 0:09:06 561k
39 796M 39 315M 0 0 900k 0 0:15:05 0:05:59 0:09:06 515k
39 796M 39 316M 0 0 900k 0 0:15:05 0:06:00 0:09:05 572k
39 796M 39 317M 0 0 900k 0 0:15:05 0:06:01 0:09:04 671k
39 796M 39 318M 0 0 900k 0 0:15:05 0:06:02 0:09:03 764k
40 796M 40 319M 0 0 900k 0 0:15:05 0:06:03 0:09:02 855k
40 796M 40 320M 0 0 900k 0 0:15:05 0:06:04 0:09:01 922k
40 796M 40 321M 0 0 901k 0 0:15:04 0:06:05 0:08:59 993k
40 796M 40 322M 0 0 901k 0 0:15:04 0:06:06 0:08:58 985k
40 796M 40 323
M 0 0 901k 0 0:15:04 0:06:07 0:08:57 962k
40 796M 40 323M 0 0 901k 0 0:15:04 0:06:08 0:08:56 948k
40 796M 40 324M 0 0 901k 0 0:15:04 0:06:09 0:08:55 938k
40 796M 40 325M 0 0 901k 0 0:15:04 0:06:10 0:08:54 877k
40 796M 40 326M 0 0 900k 0 0:15:05 0:06:11 0:08:54 833k
41 796M 41 326M 0 0 900k 0 0:15:05 0:06:12 0:08:53 817k
41 796M 41 327M 0 0 899k 0 0:15:06 0:06:13 0:08:53 790k
41 796M 41 328M 0 0 899k 0 0:15:06 0:06:14 0:08:52 781k
41 796M 41 329M 0 0 900k 0 0:15:05 0:06:15 0:08:50 833k
41 796M 41 330M 0 0 901k 0 0:15:04 0:06:16 0:08:48 933k
41 796M 41 332M 0 0 902k 0 0:15:03 0:06:17 0:08:46 1067k
41 796M 41 333M 0 0 903k 0 0:15:02 0:06:18 0:08:44 1214k
42 796M 42 334M 0 0 904k 0 0:15:00 0:06:19 0:08:41 1294k
42 796M 42 336M 0 0 906k 0 0:14:59 0:06:20 0:08:39 1345k
42 796M 42 337M 0 0 907k 0 0:14:58 0:06:21 0:08:37 1362k
42 796M 42 338M 0 0 907k 0 0:14:58 0:06:22 0:08:36 1296k
42 796M 42 339M 0 0 907k 0 0:14:58 0:06:23 0:08:35 1154k
42 796M 42 340M 0 0 906k 0 0:14:59 0:06:24 0:08:35 1049k
42 796M 42 340M 0 0 906k 0 0:14:59 0:06:25 0:08:34 946k
42 796M 42 341M 0 0 906k 0 0:14:59 0:06:26 0:08:33 877k
43 796M 43 342M 0 0 907k 0 0:14:58 0:06:27 0:08:31 883k
43 796M 43 344M 0 0 907k 0 0:14:58 0:06:28 0:08:30 958k
43 796M 43 345M 0 0 908k 0 0:14:57 0:06:29 0:08:28 1060k
43 796M 43 346M 0 0 910k 0 0:14:55 0:06:30 0:08:25 1175k
43 796M 43 348M 0 0 911k 0 0:14:54 0:06:31 0:08:23 1318k
43 796M 43 349M 0 0 913k 0 0:14:52 0:06:32 0:08:20 1438k
44 796M 44 351M 0 0 915k 0 0:14:50 0:06:33 0:08:17 1503k
44 796M 44 353M 0 0 917k 0 0:14:48 0:06:34 0:08:14 1598k
44 796M 44 354M 0 0 919k 0 0:14:46 0:06:35 0:08:11 1672k
44 796M 44 356M 0 0 921k 0 0:14:44 0:06:36 0:08:08 1654k
44 796M 44 358M 0 0 923k 0 0:14:42 0:06:37 0:08:05 1667k
45 796M 45 359M 0 0 925k 0 0:14:40 0:06:38 0:08:02 1742k
45 796M 45 361M 0 0 928k 0 0:14:38 0:06:39 0:07:59 1764k
45 796M 45 363M 0 0 929k 0 0:14:36 0:06:40 0:07:56 1731k
45 796M 45 364M 0 0 931k 0 0:14:34 0:06:41 0:07:53 1758k
46 796M 46 366M 0 0 934k 0 0:14:32 0:06:42 0:07:50 1788k
46 796M 46 368M 0 0 936k 0 0:14:30 0:06:43 0:07:47 1803k
46 796M 46 370M 0 0 938k 0 0:14:29 0:06:44 0:07:45 1724k
46 796M 46 371M 0 0 940k 0 0:14:27 0:06:45 0:07:42 1742k
46 796M 46 373M 0 0 941k 0 0:14:26 0:06:46 0:07:40 1711k
47 796M 47 374M 0 0 941k 0 0:14:25 0:06:47 0:07:38 1554k
47 796M 47 375M 0 0 942k 0 0:14:25 0:06:48 0:07:37 1410k
47 796M 47 376M 0 0 943k 0 0:14:24 0:06:49 0:07:35 1380k
47 796M 47 378M 0 0 944k 0 0:14:23 0:06:50 0:07:33 1266k
47 796M 47 379M 0 0 944k 0 0:14:22 0:06:51 0:07:31 1232k
47 796M 47 380M 0 0 945k 0 0:14:22 0:06:52 0:07:30 1247k
47 796M 47 381M 0 0 946k 0 0:14:21 0:06:53 0:07:28 1235k
48 796M 48 382M 0 0 946k 0 0:14:21 0:06:54 0:07:27 1216k
48 796M 48 384M 0 0 947k 0 0:14:20 0:06:55 0:07:25 1266k
48 796M 48 385M 0 0 948k 0 0:14:19 0:06:56 0:07:23 1244k
48 796M 48 386M 0 0 949k 0 0:14:18 0:06:57 0:07:21 1283k
48 796M 48 387M 0 0 949k 0 0:14:18 0:06:58 0:07:20 1276k
48 796M 48 388M 0 0 950k 0 0:14:17 0:06:59 0:07:18 1267k
49 796M 49 390M 0 0 951k 0 0:14:16 0:07:00 0:07:16 1241k
49 796M 49 391M 0 0 952k 0 0:14:16 0:07:01 0:07:15 1253k
49 796M 49 392M 0 0 952k 0 0:14:15 0:07:02 0:07:13 1205k
49 796M 49 393M 0 0 952k 0 0:14:15 0:07:03 0:07:12 1165k
49 796M 49 394M 0 0 952k 0 0:14:16 0:07:04 0:07:12 1091k
49 796M 49 395M 0 0 952k 0 0:14:16 0:07:05 0:07:11 1023k
49 796M 49 396M 0 0 952k 0 0:14:16 0:07:06 0:07:10 977k
49 796M 49 397M 0 0 952k 0 0:14:15 0:07:07 0:07:08 947k
49 796M 49 398M 0 0 952k 0 0:14:16 0:07:08 0:07:08 937k
50 796M 50 398M 0 0 951k 0 0:14:16 0:07:09 0:07:07 899k
50 796M 50 399M 0 0 950k 0 0:14:17 0:07:10 0:07:07 842k
50 796M 50 399M 0 0 950k 0 0:14:18 0:07:11 0:07:07 750k
50 796M 50 400M 0 0 949k 0 0:14:19 0:07:12 0:07:07 659k
50 796M 50 401M 0 0 948k 0 0:14:19 0:07:13 0:07:06 600k
50 796M 50 401M 0 0 947k 0 0:14:20 0:07:14 0:07:06 607k
50 796M 50 402M 0 0 947k 0 0:14:20 0:07:15 0:07:05 635k
50 796M 50 403M 0 0 947k 0 0:14:20 0:07:16 0:07:04 710k
50 796M 50 404M 0 0 947k 0 0:14:20 0:07:17 0:07:03 816k
50 796M 50 405M 0 0 947k 0 0:14:20 0:07:18 0:07:02 887k
51 796M 51 406M 0 0 947k 0 0:14:20 0:07:19 0:07:01 963k
51 796M 51 407M 0 0 948k 0 0:14:19 0:07:20 0:06:59 1040k
51 796M 51 408M 0 0 948k 0 0:14:19 0:07:21 0:06:58 1048k
51 796M 51 409M 0 0 948k 0 0:14:19 0:07:22 0:06:57 1068k
51 796M 51 410M 0 0 948k 0 0:14:19 0:07:23 0:06:56 1073k
51 796M 51 411M 0 0 949k 0 0:14:18 0:07:24 0:06:54 1068k
51 796M 51 412M 0 0 949k 0 0:14:18 0:07:25 0:06:53 1050k
51 796M 51 413M 0 0 949k 0 0:14:18 0:07:26 0:06:52 1053k
52 796M 52 414M 0 0 950k 0 0:14:18 0:07:27 0:06:51 1049k
52 796M 52 415M 0 0 950k 0 0:14:18 0:07:28 0:06:50 1045k
52 796M 52 416M 0 0 950k 0 0:14:18 0:07:29 0:06:49 1037k
52 796M 52 417M 0 0 950k 0 0:14:17 0:07:30 0:06:47 1034k
52 796M 52 418M 0 0 950k 0 0:14:17 0:07:31 0:06:46 1034k
52 796M 52 419M 0 0 951k 0 0:14:17 0:07:32 0:06:45 1039k
52 796M 52 420M 0 0 951k 0 0:14:17 0:07:33 0:06:44 1051k
52 796M 52 421M 0 0 951k 0 0:14:16 0:07:34 0:06:42 1067k
53 796M 53 423M 0 0 951k 0 0:14:16 0:07:35 0:06:41 1084k
53 796M 53 424M 0 0 952k 0 0:14:16 0:07:36 0:06:40 1106k
53 796M 53 425M 0 0 952k 0 0:14:15 0:07:37 0:06:38 1083k
53 796M 53 425M 0 0 951k 0 0:14:16 0:07:38 0:06:38 1020k
53 796M 53 426M 0 0 951k 0 0:14:17 0:07:39 0:06:38 914k
53 796M 53 426M 0 0 950k 0 0:14:17 0:07:40 0:06:37 814k
53 796M 53 427M 0 0 949k 0 0:14:18 0:07:41 0:06:37 693k
53 796M 53 428M 0 0 948k 0 0:14:19 0:07:42 0:06:37 592k
53 796M 53 428M 0 0 948k 0 0:14:19 0:07:43 0:06:36 591k
53 796M 53 429M 0 0 947k 0 0:14:20 0:07:44 0:06:36 643k
54 796M 54 430M 0 0 947k 0 0:14:20 0:07:45 0:06:35 677k
54 796M 54 431M 0 0 947k 0 0:14:20 0:07:46 0:06:34 742k
54 796M 54 431M 0 0 946k 0 0:14:21 0:07:47 0:06:34 788k
54 796M 54 432M 0 0 946k 0 0:14:21 0:07:48 0:06:33 779k
54 796M 54 433M 0 0 945k 0 0:14:22 0:07:49 0:06:33 746k
54 796M 54 433M 0 0 945k 0 0:14:22 0:07:50 0:06:32 713k
54 796M 54 434M 0 0 944k 0 0:14:23 0:07:51 0:06:32 694k
54 796M 54 435M 0 0 944k 0 0:14:23 0:07:52 0:06:31 722k
54 796M 54 436M 0 0 944k 0 0:14:23 0:07:53 0:06:30 795k
54 796M 54 437M 0 0 945k 0 0:14:22 0:07:54 0:06:28 895k
55 796M 55 438M 0 0 945k 0 0:14:22 0:07:55 0:06:27 986k
55 796M 55 439M 0 0 945k 0 0:14:21 0:07:56 0:06:25 1062k
55 796M 55 440M 0 0 946k 0 0:14:21 0:07:57 0:06:24 1131k
55 796M 55 442M 0 0 947k 0 0:14:20 0:07:58 0:06:22 1175k
55 796M 55 443M 0 0 947k 0 0:14:20 0:07:59 0:06:21 1158k
55 796M 55 444M 0 0 947k 0 0:14:20 0:08:00 0:06:20 1179k
55 796M 55 445M 0 0 948k 0 0:14:19 0:08:01 0:06:18 1194k
56 796M 56 446M 0 0 948k 0 0:14:19 0:08:02 0:06:17 1161k
56 796M 56 447M 0 0 949k 0 0:14:19 0:08:03 0:06:16 1143k
56 796M 56 448M 0 0 949k 0 0:14:18 0:08:04 0:06:14 1134k
56 796M 56 449M 0 0 949k 0 0:14:18 0:08:05 0:06:13 1114k
56 796M 56 450M 0 0 950k 0 0:14:18 0:08:06 0:06:12 1110k
56 796M 56 452M 0 0 950k 0 0:14:17 0:08:07 0:06:10 1102k
56 796M 56 452M 0 0 950k 0 0:14:18 0:08:08 0:06:10 1054k
56 796M 56 453M 0 0 949k 0 0:14:18 0:08:09 0:06:09 995k
57 796M 57 454M 0 0 949k 0 0:14:18 0:08:10 0:06:08 923k
57 796M 57 455M 0 0 948k 0 0:14:19 0:08:11 0:06:08 835k
57 796M 57 455M 0 0 948k 0 0:14:19 0:08:12 0:06:07 796k
57 796M 57 456M 0 0 948k 0 0:14:19 0:08:13 0:06:06 755k
57 796M 57 457M 0 0 947k 0 0:14:20 0:08:14 0:06:06 725k
57 796M 57 457M 0 0 946k 0 0:14:21 0:08:15 0:06:06 657k
57 796M 57 458M 0 0 945k 0 0:14:22 0:08:16 0:06:06 603k
57 796M 57 458M 0 0 944k 0 0:14:23 0:08:17 0:06:06 537k
57 796M 57 459M 0 0 943k 0 0:14:23 0:08:18 0:06:05 516k
57 796M 57 459M 0 0 943k 0 0:14:24 0:08:19 0:06:05 524k
57 796M 57 460M 0 0 942k 0 0:14:24 0:08:20 0:06:04 569k
57 796M 57 460M 0 0 942k 0 0:14:25 0:08:21 0:06:04 612k
57 796M 57 461M 0 0 941k 0 0:14:25 0:08:22 0:06:03 647k
58 796M 58 462M 0 0 941k 0 0:14:26 0:08:23 0:06:03 681k
58 796M 58 463M 0 0 941k 0 0:14:26 0:08:24 0:06:02 744k
58 796M 58 464M 0 0 941k 0 0:14:26 0:08:25 0:06:01 806k
58 796M 58 465M 0 0 941k 0 0:14:26 0:08:26 0:06:00 825k
58 796M 58 465M 0 0 940k 0 0:14:26 0:08:27 0:05:59 835k
58 796M 58 466M 0 0 940k 0 0:14:26 0:08:28 0:05:58 855k
58 796M 58 467M 0 0 940k 0 0:14:26 0:08:29 0:05:57 876k
58 796M 58 468M 0 0 940k 0 0:14:26 0:08:30 0:05:56 907k
59 796M 59 469M 0 0 941k 0 0:14:25 0:08:31 0:05:54 1001k
59 796M 59 470M 0 0 941k 0 0:14:25 0:08:32 0:05:53 1043k
59 796M 59 471M 0 0 941k 0 0:14:26 0:08:33 0:05:53 1044k
59 796M 59 472M 0 0 941k 0 0:14:25 0:08:34 0:05:51 1035k
59 796M 59 473M 0 0 941k 0 0:14:25 0:08:35 0:05:50 1030k
59 796M 59 474M 0 0 942k 0 0:14:25 0:08:36 0:05:49 1005k
59 796M 59 475M 0 0 942k 0 0:14:24 0:08:37 0:05:47 1041k
59 796M 59 476M 0 0 942k 0 0:14:24 0:08:38 0:05:46 1061k
60 796M 60 477M 0 0 942k 0 0:14:24 0:08:39 0:05:45 1072k
60 796M 60 478M 0 0 943k 0 0:14:24 0:08:40 0:05:44 1066k
60 796M 60 479M 0 0 943k 0 0:14:24 0:08:41 0:05:43 1028k
60 796M 60 480M 0 0 943k 0 0:14:24 0:08:42 0:05:42 1028k
60 796M 60 482M 0 0 943k 0 0:14:23 0:08:43 0:05:40 1065k
60 796M 60 483M 0 0 944k 0 0:14:23 0:08:44 0:05:39 1121k
60 796M 60 484M 0 0 945k 0 0:14:22 0:08:45 0:05:37 1198k
61 796M 61 486M 0 0 946k 0 0:14:21 0:08:46 0:05:35 1304k
61 796M 61 487M 0 0 947k 0 0:14:20 0:08:47 0:05:33 1421k
61 796M 61 489M 0 0 949k 0 0:14:18 0:08:48 0:05:30 1558k
61 796M 61 491M 0 0 951k 0 0:14:17 0:08:49 0:05:28 1646k
61 796M 61 492M 0 0 951k 0 0:14:16 0:08:50 0:05:26 1610k
62 796M 62 493M 0 0 952k 0 0:14:15 0:08:51 0:05:24 1583k
62 796M 62 495M 0 0 953k 0 0:14:15 0:08:52 0:05:23 1509k
62 796M 62 496M 0 0 953k 0 0:14:14 0:08:53 0:05:21 1391k
62 796M 62 497M 0 0 954k 0 0:14:14 0:08:54 0:05:20 1328k
62 796M 62 498M 0 0 954k 0 0:14:13 0:08:55 0:05:18 1284k
62 796M 62 499M 0 0 954k 0 0:14:13 0:08:56 0:05:17 1196k
62 796M 62 500M 0 0 954k 0 0:14:13 0:08:57 0:05:16 1121k
63 796M 63 501M 0 0 955k 0 0:14:13 0:08:58 0:05:15 1099k
63 796M 63 502M 0 0 955k 0 0:14:13 0:08:59 0:05:14 1044k
63 796M 63 503M 0 0 955k 0 0:14:13 0:09:00 0:05:13 989k
63 796M 63 504M 0 0 954k 0 0:14:14 0:09:01 0:05:13 936k
63 796M 63 505M 0 0 954k 0 0:14:14 0:09:02 0:05:12 898k
63 796M 63 506M 0 0 954k 0 0:14:14 0:09:03 0:05:11 855k
63 796M 63 507M 0 0 954k 0 0:14:14 0:09:04 0:05:10 837k
63 796M 63 508M 0 0 954k 0 0:14:14 0:09:05 0:05:09 875k
63 796M 63 509M 0 0 954k 0 0:14:14 0:09:06 0:05:08 957k
64 796M 64 509M 0 0 954k 0 0:14:14 0:09:07 0:05:07 978k
64 796M 64 510M 0 0 954k 0 0:14:14 0:09:08 0:05:06 939k
64 796M 64 511M 0 0 953k 0 0:14:14 0:09:09 0:05:05 888k
64 796M 64 512M 0 0 953k 0 0:14:15 0:09:10 0:05:05 859k
64 796M 64 512M 0 0 953k 0 0:14:15 0:09:11 0:05:04 804k
64 796M 64 513M 0 0 952k 0 0:14:15 0:09:12 0:05:03 756k
64 796M 64 514M 0 0 951k 0 0:14:16 0:09:13 0:05:03 705k
64 796M 64 514M 0 0 951k 0 0:14:17 0:09:14 0:05:03 648k
64 796M 64 515M 0 0 950k 0 0:14:17 0:09:15 0:05:02 617k
64 796M 64 516M 0 0 950k 0 0:14:17 0:09:16 0:05:01 624k
64 796M 64 516M 0 0 950k 0 0:14:18 0:09:17 0:05:01 658k
64 796M 64 517M 0 0 949k 0 0:14:18 0:09:18 0:05:00 685k
65 796M 65 517M 0 0 948k 0 0:14:19 0:09:19 0:05:00 670k
65 796M 65 518M 0 0 947k 0 0:14:20 0:09:20 0:05:00 624k
65 796M 65 518M 0 0 946k 0 0:14:21 0:09:21 0:05:00 545k
65 796M 65 519M 0 0 945k 0 0:14:22 0:09:22 0:05:00 474k
65 796M 65 519M 0 0 945k 0 0:14:22 0:09:23 0:04:59 462k
65 796M 65 520M 0 0 944k 0 0:14:23 0:09:24 0:04:59 516k
65 796M 65 521M 0 0 944k 0 0:14:23 0:09:25 0:04:58 597k
65 796M 65 521M 0 0 944k 0 0:14:23 0:09:26 0:04:57 658k
65 796M 65 522M 0 0 943k 0 0:14:24 0:09:27 0:04:57 663k
65 796M 65 522M 0 0 942k 0 0:14:25 0:09:28 0:04:57 651k
65 796M 65 523M 0 0 941k 0 0:14:25 0:09:29 0:04:56 610k
65 796M 65 523M 0 0 941k 0 0:14:26 0:09:30 0:04:56 563k
65 796M 65 524M 0 0 940k 0 0:14:26 0:09:31 0:04:55 564k
66 796M 66 525M 0 0 940k 0 0:14:26 0:09:32 0:04:54 641k
66 796M 66 526M 0 0 940k 0 0:14:26 0:09:33 0:04:53 740k
66 796M 66 527M 0 0 940k 0 0:14:26 0:09:34 0:04:52 851k
66 796M 66 528M 0 0 940k 0 0:14:26 0:09:35 0:04:51 875k
66 796M 66 528M 0 0 939k 0 0:14:27 0:09:36 0:04:51 836k
66 796M 66 529M 0 0 938k 0 0:14:28 0:09:37 0:04:51 731k
66 796M 66 529M 0 0 937k 0 0:14:29 0:09:38 0:04:51 608k
66 796M 66 529M 0 0 937k 0 0:14:29 0:09:39 0:04:50 504k
66 796M 66 530M 0 0 936k 0 0:14:30 0:09:40 0:04:50 473k
66 796M 66 531M 0 0 936k 0 0:14:31 0:09:41 0:04:50 491k
66 796M 66 531M 0 0 935k 0 0:14:31 0:09:42 0:04:49 566k
66 796M 66 532M 0 0 935k 0 0:14:31 0:09:43 0:04:48 657k
67 796M 67 533M 0 0 935k 0 0:14:31 0:09:44 0:04:47 720k
67 796M 67 534M 0 0 935k 0 0:14:31 0:09:45 0:04:46 783k
67 796M 67 535M 0 0 935k 0 0:14:31 0:09:46 0:04:45 854k
67 796M 67 536M 0 0 935k 0 0:14:31 0:09:47 0:04:44 926k
67 796M 67 537M 0 0 936k 0 0:14:30 0:09:48 0:04:42 1001k
67 796M 67 538M 0 0 936k 0 0:14:30 0:09:49 0:04:41 1058k
67 796M 67 539M 0 0 936k 0 0:14:30 0:09:50 0:04:40 1116k
67 796M 67 540M 0 0 936k 0 0:14:30 0:09:51 0:04:39 1107k
68 796M 68 541M 0 0 936k 0 0:14:30 0:09:52 0:04:38 1059k
68 796M 68 542M 0 0 936k 0 0:14:30 0:09:53 0:04:37 1009k
68 796M 68 543M 0 0 937k 0 0:14:30 0:09:54 0:04:36 1011k
68 796M 68 544M 0 0 937k 0 0:14:29 0:09:55 0:04:34 1021k
68 796M 68 545M 0 0 937k 0 0:14:29 0:09:56 0:04:33 1040k
68 796M 68 546M 0 0 937k 0 0:14:29 0:09:57 0:04:32 1065k
68 796M 68 547M 0 0 937k 0 0:14:29 0:09:58 0:04:31 1060k
68 796M 68 548M 0 0 937k 0 0:14:29 0:09:59 0:04:30 1002k
68 796M 68 549M 0 0 937k 0 0:14:29 0:10:00 0:04:29 926k
69 796M 69 550M 0
0 937k 0 0:14:29 0:10:01 0:04:28 880k
69 796M 69 550M 0 0 936k 0 0:14:30 0:10:02 0:04:28 772k
69 796M 69 551M 0 0 935k 0 0:14:31 0:10:03 0:04:28 699k
69 796M 69 551M 0 0 935k 0 0:14:31 0:10:04 0:04:27 628k
69 796M 69 552M 0 0 934k 0 0:14:32 0:10:05 0:04:27 564k
69 796M 69 552M 0 0 933k 0 0:14:32 0:10:06 0:04:26 543k
69 796M 69 553M 0 0 933k 0 0:14:33 0:10:07 0:04:26 626k
69 796M 69 554M 0 0 933k 0 0:14:33 0:10:08 0:04:25 699k
69 796M 69 555M 0 0 934k 0 0:14:32 0:10:09 0:04:23 829k
69 796M 69 556M 0 0 934k 0 0:14:32 0:10:10 0:04:22 972k
70 796M 70 557M 0 0 934k 0 0:14:32 0:10:11 0:04:21 1025k
70 796M 70 558M 0 0 934k 0 0:14:32 0:10:12 0:04:20 1000k
70 796M 70 559M 0 0 934k 0 0:14:32 0:10:13 0:04:19 966k
70 796M 70 560M 0 0 934k 0 0:14:32 0:10:14 0:04:18 923k
70 796M 70 561M 0 0 934k 0 0:14:32 0:10:15 0:04:17 873k
70 796M 70 562M 0 0 934k 0 0:14:32 0:10:16 0:04:16 884k
70 796M 70 563M 0 0 934k 0 0:14:32 0:10:17 0:04:15 943k
70 796M 70 563M 0 0 934k 0 0:14:32 0:10:18 0:04:14 975k
70 796M 70 565M 0 0 934k 0 0:14:32 0:10:19 0:04:13 1001k
71 796M 71 566M 0 0 934k 0 0:14:32 0:10:20 0:04:12 1017k
71 796M 71 567M 0 0 934k 0 0:14:32 0:10:21 0:04:11 1011k
71 796M 71 567M 0 0 934k 0 0:14:32 0:10:22 0:04:10 979k
71 796M 71 568M 0 0 934k 0 0:14:32 0:10:23 0:04:09 951k
71 796M 71 569M 0 0 934k 0 0:14:32 0:10:24 0:04:08 904k
71 796M 71 570M 0 0 934k 0 0:14:32 0:10:25 0:04:07 845k
71 796M 71 571M 0 0 934k 0 0:14:32 0:10:26 0:04:06 824k
71 796M 71 572M 0 0 934k 0 0:14:32 0:10:27 0:04:05 858k
71 796M 71 572M 0 0 934k 0 0:14:32 0:10:28 0:04:04 874k
72 796M 72 573M 0 0 933k 0 0:14:32 0:10:29 0:04:03 877k
72 796M 72 574M 0 0 933k 0 0:14:32 0:10:30 0:04:02 909k
72 796M 72 575M 0 0 933k 0 0:14:33 0:10:31 0:04:02 869k
72 796M 72 575M 0 0 932k 0 0:14:34 0:10:32 0:04:02 748k
72 796M 72 575M 0 0 931k 0 0:14:35 0:10:33 0:04:02 627k
72 796M 72 576M 0 0 930k 0 0:14:35 0:10:34 0:04:01 545k
72 796M 72 576M 0 0 930k 0 0:14:36 0:10:35 0:04:01 477k
72 796M 72 577M 0 0 929k 0 0:14:36 0:10:36 0:04:00 489k
72 796M 72 578M 0 0 929k 0 0:14:36 0:10:37 0:03:59 581k
72 796M 72 579M 0 0 929k 0 0:14:37 0:10:38 0:03:59 654k
72 796M 72 579M 0 0 929k 0 0:14:37 0:10:39 0:03:58 702k
72 796M 72 580M 0 0 928k 0 0:14:37 0:10:40 0:03:57 748k
73 796M 73 581M 0 0 928k 0 0:14:37 0:10:41 0:03:56 800k
73 796M 73 582M 0 0 928k 0 0:14:37 0:10:42 0:03:55 792k
73 796M 73 583M 0 0 928k 0 0:14:37 0:10:43 0:03:54 840k
73 796M 73 584M 0 0 928k 0 0:14:37 0:10:44 0:03:53 877k
73 796M 73 585M 0 0 928k 0 0:14:37 0:10:45 0:03:52 919k
73 796M 73 586M 0 0 929k 0 0:14:37 0:10:46 0:03:51 957k
73 796M 73 587M 0 0 929k 0 0:14:37 0:10:47 0:03:50 1012k
73 796M 73 588M 0 0 929k 0 0:14:37 0:10:48 0:03:49 1011k
73 796M 73 589M 0 0 929k 0 0:14:37 0:10:49 0:03:48 1030k
74 796M 74 589M 0 0 929k 0 0:14:37 0:10:50 0:03:47 997k
74 796M 74 590M 0 0 929k 0 0:14:37 0:10:51 0:03:46 958k
74 796M 74 591M 0 0 929k 0 0:14:37 0:10:52 0:03:45 904k
74 796M 74 592M 0 0 929k 0 0:14:37 0:10:53 0:03:44 891k
74 796M 74 593M 0 0 928k 0 0:14:37 0:10:54 0:03:43 864k
74 796M 74 594M 0 0 928k 0 0:14:37 0:10:55 0:03:42 846k
74 796M 74 594M 0 0 928k 0 0:14:38 0:10:56 0:03:42 821k
74 796M 74 595M 0 0 928k 0 0:14:38 0:10:57 0:03:41 816k
74 796M 74 596M 0 0 928k 0 0:14:38 0:10:58 0:03:40 807k
74 796M 74 597M 0 0 927k 0 0:14:38 0:10:59 0:03:39 762k
75 796M 75 597M 0 0 927k 0 0:14:39 0:11:00 0:03:39 709k
75 796M 75 597M 0 0 926k 0 0:14:40 0:11:01 0:03:39 613k
75 796M 75 598M 0 0 925k 0 0:14:41 0:11:02 0:03:39 502k
75 796M 75 598M 0 0 924k 0 0:14:41 0:11:03 0:03:38 427k
75 796M 75 599M 0 0 923k 0 0:14:42 0:11:04 0:03:38 404k
75 796M 75 599M 0 0 923k 0 0:14:43 0:11:05 0:03:38 398k
75 796M 75 599M 0 0 922k 0 0:14:43 0:11:06 0:03:37 411k
75 796M 75 600M 0 0 921k 0 0:14:44 0:11:07 0:03:37 442k
75 796M 75 600M 0 0 921k 0 0:14:45 0:11:08 0:03:37 484k
75 796M 75 601M 0 0 920k 0 0:14:45 0:11:09 0:03:36 515k
75 796M 75 602M 0 0 920k 0 0:14:45 0:11:10 0:03:35 563k
75 796M 75 603M 0 0 920k 0 0:14:45 0:11:11 0:03:34 656k
75 796M 75 604M 0 0 920k 0 0:14:45 0:11:12 0:03:33 763k
75 796M 75 604M 0 0 920k 0 0:14:45 0:11:13 0:03:32 824k
76 796M 76 606M 0 0 920k 0 0:14:45 0:11:14 0:03:31 912k
76 796M 76 607M 0 0 920k 0 0:14:45 0:11:15 0:03:30 997k
76 796M 76 608M 0 0 921k 0 0:14:44 0:11:16 0:03:28 1078k
76 796M 76 609M 0 0 921k 0 0:14:44 0:11:17 0:03:27 1108k
76 796M 76 610M 0 0 921k 0 0:14:44 0:11:18 0:03:26 1121k
76 796M 76 611M 0 0 922k 0 0:14:44 0:11:19 0:03:25 1119k
76 796M 76 612M 0 0 922k 0 0:14:43 0:11:20 0:03:23 1109k
77 796M 77 613M 0 0 922k 0 0:14:43 0:11:21 0:03:22 1063k
77 796M 77 614M 0 0 922k 0 0:14:43 0:11:22 0:03:21 1075k
77 796M 77 615M 0 0 923k 0 0:14:43 0:11:23 0:03:20 1084k
77 796M 77 616M 0 0 923k 0 0:14:43 0:11:24 0:03:19 1070k
77 796M 77 617M 0 0 922k 0 0:14:43 0:11:25 0:03:18 999k
77 796M 77 618M 0 0 922k 0 0:14:43 0:11:26 0:03:17 955k
77 796M 77 618M 0 0 922k 0 0:14:43 0:11:27 0:03:16 863k
77 796M 77 619M 0 0 922k 0 0:14:43 0:11:28 0:03:15 842k
77 796M 77 620M 0 0 922k 0 0:14:43 0:11:29 0:03:14 849k
78 796M 78 621M 0 0 922k 0 0:14:43 0:11:30 0:03:13 877k
78 796M 78 622M 0 0 922k 0 0:14:43 0:11:31 0:03:12 919k
78 796M 78 623M 0 0 922k 0 0:14:43 0:11:32 0:03:11 980k
78 796M 78 624M 0 0 923k 0 0:14:43 0:11:33 0:03:10 996k
78 796M 78 625M 0 0 923k 0 0:14:43 0:11:34 0:03:09 987k
78 796M 78 626M 0 0 923k 0 0:14:43 0:11:35 0:03:08 1006k
78 796M 78 627M 0 0 923k 0 0:14:42 0:11:36 0:03:06 1026k
78 796M 78 628M 0 0 924k 0 0:14:42 0:11:37 0:03:05 1071k
79 796M 79 630M 0 0 924k 0 0:14:41 0:11:38 0:03:03 1129k
79 796M 79 631M 0 0 924k 0 0:14:41 0:11:39 0:03:02 1142k
79 796M 79 632M 0 0 924k 0 0:14:41 0:11:40 0:03:01 1159k
79 796M 79 633M 0 0 925k 0 0:14:41 0:11:41 0:03:00 1167k
79 796M 79 634M 0 0 925k 0 0:14:40 0:11:42 0:02:58 1178k
79 796M 79 635M 0 0 926k 0 0:14:40 0:11:43 0:02:57 1159k
80 796M 80 637M 0 0 926k 0 0:14:39 0:11:44 0:02:55 1218k
80 796M 80 638M
0 0 927k 0 0:14:39 0:11:45 0:02:54 1246k
80 796M 80 639M 0 0 927k 0 0:14:39 0:11:46 0:02:53 1247k
80 796M 80 640M 0 0 928k 0 0:14:38 0:11:47 0:02:51 1235k
80 796M 80 641M 0 0 928k 0 0:14:38 0:11:48 0:02:50 1231k
80 796M 80 642M 0 0 928k 0 0:14:38 0:11:49 0:02:49 1159k
80 796M 80 643M 0 0 928k 0 0:14:37 0:11:50 0:02:47 1148k
81 796M 81 645M 0 0 929k 0 0:14:37 0:11:51 0:02:46 1146k
81 796M 81 646M 0 0 929k 0 0:14:36 0:11:52 0:02:44 1178k
81 796M 81 648M 0 0 930k 0 0:14:36 0:11:53 0:02:43 1255k
81 796M 81 649M 0 0 931k 0 0:14:34 0:11:54 0:02:40 1413k
81 796M 81 650M
0 0 932k 0 0:14:34 0:11:55 0:02:39 1406k
81 796M 81 651M 0 0 932k 0 0:14:34 0:11:56 0:02:38 1394k
81 796M 81 652M 0 0 932k 0 0:14:34 0:11:57 0:02:37 1306k
82 796M 82 653M 0 0 932k 0 0:14:34 0:11:58 0:02:36 1200k
82 796M 82 654M 0 0 932k 0 0:14:34 0:11:59 0:02:35 995k
82 796M 82 655M 0 0 932k 0 0:14:34 0:12:00 0:02:34 933k
82 796M 82 656M 0 0 932k 0 0:14:34 0:12:01 0:02:33 897k
82 796M 82 657M 0 0 932k 0 0:14:34 0:12:02 0:02:32 922k
82 796M 82 658M 0 0 932k 0 0:14:34 0:12:03 0:02:31 937k
82 796M 82 659M 0 0 932k 0 0:14:34 0:12:04 0:02:30 1014k
82 796M 82 660M 0 0 932k 0 0:14:33 0:12:05 0:02:28 1050k
83 796M 83 661M 0 0 933k 0 0:14:33 0:12:06 0:02:27 1077k
83 796M 83 662M 0 0 933k 0 0:14:33 0:12:07 0:02:26 1055k
83 796M 83 663M 0 0 933k 0 0:14:33 0:12:08 0:02:25 1040k
83 796M 83 664M 0 0 933k 0 0:14:33 0:12:09 0:02:24 1007k
83 796M 83 665M 0 0 933k 0 0:14:33 0:12:10 0:02:23 1006k
83 796M 83 666M 0 0 933k 0 0:14:33 0:12:11 0:02:22 976k
83 796M 83 667M 0 0 933k 0 0:14:33 0:12:12 0:02:21 985k
83 796M 83 668M 0 0 933k 0 0:14:33 0:12:13 0:02:20 971k
84 796M 84 669M 0 0 933k 0 0:14:33 0:12:14 0:02:19 996k
84 796M 84 670M 0 0 933k 0 0:14:33 0:12:15 0:02:18 977k
84 796M 84 671M 0 0 933k 0 0:14:33 0:12:16 0:02:17 987k
84 796M 84 672M 0 0 934k 0 0:14:32 0:12:17 0:02:15 1006k
84 796M 84 673M 0 0 934k 0 0:14:32 0:12:18 0:02:14 1071k
84 796M 84 674M 0 0 935k 0 0:14:31 0:12:19 0:02:12 1146k
84 796M 84 676M 0 0 935k 0 0:14:31 0:12:20 0:02:11 1261k
85 796M 85 677M 0 0 936k 0 0:14:30 0:12:21 0:02:09 1291k
85 796M 85 678M 0 0 936k 0 0:14:30 0:12:22 0:02:08 1284k
85 796M 85 679M 0 0 936k 0 0:14:30 0:12:23 0:02:07 1267k
85 796M 85 680M 0 0 936k 0 0:14:30 0:12:24 0:02:06 1146k
85 796M 85 681M 0 0 936k 0 0:14:30 0:12:25 0:02:05 989k
85 796M 85 681M 0 0 935k 0 0:14:31 0:12:26 0:02:05 896k
85 796M 85 682M 0 0 935k 0 0:14:31 0:12:27 0:02:04 817k
85 796M 85 683M 0 0 935k 0 0:14:31 0:12:28 0:02:03 710k
85 796M 85 683M 0 0 934k 0 0:14:32 0:12:29 0:02:03 660k
85 796M 85 684M 0 0 934k 0 0:14:32 0:12:30 0:02:02 642k
86 796M 86 684M 0 0 933k 0 0:14:32 0:12:31 0:02:01 642k
86 796M 86 685M 0 0 933k 0 0:14:33 0:12:32 0:02:01 656k
86 796M 86 686M 0 0 933k 0 0:14:33 0:12:33 0:02:00 711k
86 796M 86 687M 0 0 933k 0 0:14:32 0:12:34 0:01:58 812k
86 796M 86 688M 0 0 934k 0 0:14:32 0:12:35 0:01:57 944k
86 796M 86 690M 0 0 934k 0 0:14:32 0:12:36 0:01:56 1050k
86 796M 86 691M 0 0 935k 0 0:14:31 0:12:37 0:01:54 1132k
86 796M 86 692M 0 0 935k 0 0:14:31 0:12:38 0:01:53 1208k
87 796M 87 693M 0 0 935k 0 0:14:31 0:12:39 0:01:52 1156k
87 796M 87 694M 0 0 935k 0 0:14:31 0:12:40 0:01:51 1070k
87 796M 87 695M 0 0 935k 0 0:14:31 0:12:41 0:01:50 1000k
87 796M 87 695M 0 0 934k 0 0:14:32 0:12:42 0:01:50 883k
87 796M 87 696M 0 0 934k 0 0:14:32 0:12:43 0:01:49 746k
87 796M 87 696M 0 0 934k 0 0:14:32 0:12:44 0:01:48 729k
87 796M 87 697M 0 0 934k 0 0:14:32 0:12:45 0:01:47 750k
87 796M 87 698M 0 0 934k 0 0:14:32 0:12:46 0:01:46 806k
87 796M 87 699M 0 0 934k 0 0:14:32 0:12:47 0:01:45 885k
88 796M 88 700M 0 0 934k 0 0:14:32 0:12:48 0:01:44 961k
88 796M 88 701M 0 0 934k 0 0:14:32 0:12:49 0:01:43 972k
88 796M 88 702M 0 0 934k 0 0:14:32 0:12:50 0:01:42 942k
88 796M 88 703M 0 0 933k 0 0:14:33 0:12:51 0:01:42 872k
88 796M 88 703M 0 0 933k 0 0:14:33 0:12:52 0:01:41 819k
88 796M 88 704M 0 0 933k 0 0:14:33 0:12:53 0:01:40 763k
88 796M 88 705M 0 0 933k 0 0:14:33 0:12:54 0:01:39 781k
88 796M 88 706M 0 0 933k 0 0:14:33 0:12:55 0:01:38 836k
88 796M 88 707M 0 0 933k 0 0:14:33 0:12:56 0:01:37 903k
88 796M 88 708M 0 0 933k 0 0:14:33 0:12:57 0:01:36 888k
89 796M 89 708M 0 0 933k 0 0:14:33 0:12:58 0:01:35 890k
89 796M 89 709M 0 0 932k 0 0:14:33 0:12:59 0:01:34 868k
89 796M 89 710M 0 0 932k 0 0:14:34 0:13:00 0:01:34 799k
89 796M 89 711M 0 0 932k 0 0:14:34 0:13:01 0:01:33 711k
89 796M 89 711M 0 0 931k 0 0:14:35 0:13:02 0:01:33 657k
89 796M 89 711M 0 0 931k 0 0:14:35 0:13:03 0:01:32 617k
89 796M 89 712M 0 0 930k 0 0:14:35 0:13:04 0:01:31 590k
89 796M 89 713M 0 0 930k 0 0:14:36 0:13:05 0:01:31 610k
89 796M 89 714M 0 0 930k 0 0:14:36 0:13:06 0:01:30 643k
89 796M 89 714M 0 0 930k 0 0:14:36 0:13:07 0:01:29 718k
89 796M 89 715M 0 0 930k 0 0:14:36 0:13:08 0:01:28 762k
90 796M 90 716M 0 0 929k 0 0:14:36 0:13:09 0:01:27 811k
90 796M 90 717M 0 0 930k 0 0:14:36 0:13:10 0:01:26 855k
90 796M 90 718M 0 0 930k 0 0:14:36 0:13:11 0:01:25 909k
90 796M 90 719M 0 0 930k 0 0:14:36 0:13:12 0:01:24 940k
90 796M 90 720M 0 0 930k 0 0:14:36 0:13:13 0:01:23 961k
90 796M 90 721M 0 0 930k 0 0:14:36 0:13:14 0:01:22 980k
90 796M 90 722M 0 0 930k 0 0:14:36 0:13:15 0:01:21 942k
90 796M 90 723M 0 0 930k 0 0:14:36 0:13:16 0:01:20 894k
90 796M 90 723M 0 0 930k 0 0:14:36 0:13:17 0:01:19 895k
91 796M 91 724M 0 0 930k 0 0:14:36 0:13:18 0:01:18 915k
91 796M 91 725M 0 0 930k 0 0:14:36 0:13:19 0:01:17 911k
91 796M 91 726M 0 0 930k 0 0:14:36 0:13:20 0:01:16 957k
91 796M 91 728M 0 0 930k 0 0:14:35 0:13:21 0:01:14 1032k
91 796M 91 729M 0 0 931k 0 0:14:35 0:13:22 0:01:13 1118k
91 796M 91 730M 0 0 931k 0 0:14:34 0:13:23 0:01:11 1222k
91 796M 91 732M 0 0 932k 0 0:14:33 0:13:24 0:01:09 1360k
92 796M 92 734M 0 0 933k 0 0:14:33 0:13:25 0:01:08 1480k
92 796M 92 735M 0 0 934k 0 0:14:32 0:13:26 0:01:06 1562k
92 796M 92 737M 0 0 935k 0 0:14:31 0:13:27 0:01:04 1642k
92 796M 92 739M 0 0 936k 0 0:14:30 0:13:28 0:01:02 1724k
93 796M 93 740M 0 0 937k 0 0:14:29 0:13:29 0:01:00 1735k
93 796M 93 742M 0 0 938k 0 0:14:29 0:13:30 0:00:59 1640k
93 796M 93 743M 0 0 938k 0 0:14:28 0:13:31 0:00:57 1536k
93 796M 93 744M 0 0 938k 0 0:14:28 0:13:32 0:00:56 1355k
93 796M 93 744M 0 0 938k 0 0:14:29 0:13:33 0:00:56 1127k
93 796M 93 745M 0 0 937k 0 0:14:29 0:13:34 0:00:55 886k
93 796M 93 745M 0 0 937k 0 0:14:29 0:13:35 0:00:54 782k
93 796M 93 746M 0 0 937k 0 0:14:30 0:13:36 0:00:54 730k
93 796M 93 747M 0 0 937k 0 0:14:30 0:13:37 0:00:53 749k
94 796M 94 748M 0 0 937k 0 0:14:29 0:13:38 0:00:51 829k
94 796M 94 750M 0 0 937k 0 0:14:29 0:13:39 0:00:50 986k
94 796M 94 751M 0 0 938k 0 0:14:28 0:13:40 0:00:48 1151k
94 796M 94 752M 0 0 939k 0 0:14:28 0:13:41 0:00:47 1257k
94 796M 94 754M 0 0 939k 0 0:14:27 0:13:42 0:00:45 1362k
94 796M 94 755M 0 0 940k 0 0:14:27 0:13:43 0:00:44 1433k
95 796M 95 757M 0 0 940k 0 0:14:26 0:13:44 0:00:42 1451k
95 796M 95 758M 0 0 941k 0 0:14:26 0:13:45 0:00:41 1388k
95 796M 95 759M 0 0 941k 0 0:14:25 0:13:46 0:00:39 1364k
95 796M 95 760M 0 0 942k 0 0:14:25 0:13:47 0:00:38 1334k
95 796M 95 762M 0 0 942k 0 0:14:25 0:13:48 0:00:37 1275k
95 796M 95 763M 0 0 942k 0 0:14:24 0:13:49 0:00:35 1271k
96 796M 96 764M 0 0 943k 0 0:14:24 0:13:50 0:00:34 1321k
96 796M 96 766M 0 0 944k 0 0:14:23 0:13:51 0:00:32 1384k
96 796M 96 768M 0 0 945k 0 0:14:22 0:13:52 0:00:30 1455k
96 796M 96 769M 0 0 946k 0 0:14:21 0:13:53 0:00:28 1582k
96 796M 96 771M 0 0 947k 0 0:14:20 0:13:54 0:00:26 1631k
97 796M 97 772M 0 0 947k 0 0:14:20 0:13:55 0:00:25 1610k
97 796M 97 774M 0 0 948k 0 0:14:19 0:13:56 0:00:23 1585k
97 796M 97 775M 0 0 948k 0 0:14:19 0:13:57 0:00:22 1482k
97 796M 97 776M 0 0 948k 0 0:14:19 0:13:58 0:00:21 1346k
97 796M 97 777M 0 0 948k 0 0:14:19 0:13:59 0:00:20 1234k
97 796M 97 778M 0 0 948k 0 0:14:19 0:14:00 0:00:19 1159k
97 796M 97 779M 0 0 949k 0 0:14:19 0:14:01 0:00:18 1101k
98 796M 98 780M 0 0 949k 0 0:14:18 0:14:02 0:00:16 1109k
98 796M 98 781M 0 0 949k 0 0:14:18 0:14:03 0:00:15 1133k
98 796M 98 782M 0 0 949k 0 0:14:18 0:14:04 0:00:14 1149k
98 796M 98 784M 0 0 950k 0 0:14:18 0:14:05 0:00:13 1164k
98 796M 98 785M 0 0 950k 0 0:14:18 0:14:06 0:00:12 1160k
98 796M 98 786M 0 0 950k 0 0:14:17 0:14:07 0:00:10 1163k
98 796M 98 787M 0 0 950k 0 0:14:17 0:14:08 0:00:09 1139k
99 796M 99 788M 0 0 951k 0 0:14:17 0:14:09 0:00:08 1170k
99 796M 99 789M 0 0 951k 0 0:14:16 0:14:10 0:00:06 1213k
99 796M 99 790M 0 0 951k 0 0:14:16 0:14:11 0:00:05 1204k
99 796M 99 791M 0 0 951k 0 0:14:16 0:14:12 0:00:04 1120k
99 796M 99 792M 0 0 951k 0 0:14:16 0:14:13 0:00:03 1061k
99 796M 99 793M 0 0 951k 0 0:14:16 0:14:14 0:00:02 997k
99 796M 99 794M 0 0 951k 0 0:14:16 0:14:15 0:00:01 939k
99 796M 99 795M 0 0 951k 0 0:14:16 0:14:16 --:--:-- 927k
100 796M 100 796M 0 0 951k 0 0:14:16 0:14:16 --:--:-- 968k
Once the downloaded is complete, extract the file and set the environment variable PYSYN_CDBS to the path of the trds subdirectory. The next cell will do this for you, as long as the .tar file downloaded above has not been moved.
tar_archive = 'hlsp_reference-atlases_hst_multi_everything_multi_v11_sed.tar'
extract_to = 'hlsp_reference-atlases_hst_multi_everything_multi_v11_sed'
abs_extract_to = os.path.abspath(extract_to)
with tarfile.open(tar_archive, 'r') as tar:
for member in tar.getmembers():
member_path = os.path.abspath(os.path.join(abs_extract_to, member.name))
if member_path.startswith(abs_extract_to):
tar.extract(member, path=extract_to)
else:
print(f"Skipped {member.name} due to potential security risk")
os.environ['PYSYN_CDBS'] = os.path.join(abs_extract_to, 'grp/redcat/trds/')
Now, after having set up PYSYN_CDBS, we import stsynphot. A warning regarding the Vega spectrum is expected here.
import stsynphot as stsyn
WARNING: Failed to load Vega spectrum from /home/runner/work/hst_notebooks/hst_notebooks/notebooks/WFC3/flux_conversion_tool/hlsp_reference-atlases_hst_multi_everything_multi_v11_sed/grp/redcat/trds//calspec/alpha_lyr_stis_010.fits; Functionality involving Vega will be cripped: FileNotFoundError(2, 'No such file or directory') [stsynphot.spectrum]
2. Input and output setup#
2.1 Units#
The conversion framework below will accept any astropy or synphot unit with dimensions of spectral flux density (\(F_\lambda\) or \(F_\nu\)) or photon flux density. Flux units with any of the following dimensions will be supported by the tool:
[power] [area] [wavelength]\(^{-1}\)
[power] [area] [frequency]\(^{-1}\)
photons [area] [wavelength]\(^{-1}\)
photons [area] [frequency]\(^{-1}\)
Alternatively, a magnitude system may be specified as the unit for the input or the output in the same way that a flux density would be. The tables below lists flux units which are defined by name in astropy and synphot, and the magnitude systems supported by the tool.
Unit |
Definition |
astropy/synphot attribute |
|---|---|---|
Jansky |
$\(10^{-26} \text{ W} \text{ m}^{-2} \text{ Hz}^{-1}\)$ |
|
fnu |
$\(\text{erg} \text{ s}^{-1} \text{ cm}^{-2} \text{ Hz}^{-1}\)$ |
|
flam |
$\(\text{erg} \text{ s}^{-1} \text{ cm}^{-2} \text{ Å}^{-1}\)$ |
|
photnu |
$\(\text{photons} \text{ s}^{-1} \text{ cm}^{-2} \text{ Hz}^{-1}\)$ |
|
photlam |
$\(\text{photons} \text{ s}^{-1} \text{ cm}^{-2} \text{ Å}^{-1}\)$ |
|
Mag System |
astropy/synphot attribute |
|---|---|
ABmag |
|
STmag |
|
vegamag |
|
For more information on accepted units in synphot, refer to the documentation here.
2.2 Bandpasses#
When selecting a magnitude as an input or output, the tool will need a bandpass to be defined, which is done with a string of observation mode, or obsmode, keywords. The pivot wavelength for that bandpass will then serve as the characteristic wavelength to be used for the conversion.
For HST bandpasses, stsynphot accounts for the telescope’s optics by combining throughput information along the entire optical path. As an example, 'wfc3, uvis2, f475w, mjd#59367' tells stsynphot to retrieve the latest throughput tables for the UVIS2 detector on WFC3, through the F475W filter for the Modified Julian Date 59367 (June 1, 2021). The option to specify a Julian date is provided for instruments which show changes in sensitivity over time. If no date is specified, stsynphot will use the reference epoch for each instrument as default.
As the required and optional obsmode keywords vary from instrument to instrument, it would be impractical to list the available options here in their entirety. Please refer to the full list of available obsmode keywords for details on how to specify HST bandpasses.
For non-HST filter systems, the only required keywords are the filter system’s name and that of the desired filter within that system (e.g. 'johnson, v'). A list of the non-HST filter systems accepted by stsynphot is given here:
System |
Bands |
|---|---|
cousins |
r, i |
galex |
nuv, fuv |
johnson |
u, b, v, r, i, j, k |
landolt |
u, b, v, r, i |
sdss |
u, g, r, i, z, |
stromgren |
u, v, b, y |
2.3 Choosing a spectrum#
You’ll also need to define a spectrum, which the tool will use to extrapolate your input flux to an output at a different wavelength.
The embedded code below shows how to generate or load various useful spectra. You can simply copy one of them into the cell below and modify as appropriate, or create your own. For more information, see the Source Spectrum documentation.
Some notes:
For evaluation and plotting, these models default to outputting flux in photlam, however, the output unit may be specified with the
flux_unitkeyword argument.synphot.models.BlackBody1Doutputs a function according to Planck’s law, which means that the output unit carries an implicit “per unit solid angle,” in steradians. For a normalized blackbody, you can useBlackBodyNorm1D, whose output is normalized to a 1 solar radius star at a distance of 1 kpc, or multiply your source spectrum by some solid angle of your choosing.synphot.models.PowerLawFlux1Duses the definition \(f(x) = A (\frac{x}{x_0})^{-\alpha}\), where \(A\) is input flux (flux_in), and \(x_0\) is the input wavelength (wavelength_in). Note the negative sign in front of the power law index \(\alpha\). The model can generate curves with \(x\) as either frequency or wavelength, but the example here assumes that wavelength will be used. The y-axis unit will be taken from \(A\).A wide array of reference spectra are available for download from spectral atlases located here.
Example spectrum definitions:
# Blackbody
bb_temp = 5800 * u.K
model = BlackBody1D(bb_temp)
spectrum = SourceSpectrum(model)
# Power law
pl_index = 0
model = PowerLawFlux1D(amplitude=flux_in, x_0=wavelength_in, alpha=pl_index)
spectrum = SourceSpectrum(model)
# Load from a FITS table
spectrum = SourceSpectrum.from_file('/path/to/your/spectrum.fits')
The notebook has been set up to perform an extrapolation from \(V = 0.0\) in the Vega system to the R-band in the same system, using the Vega spectrum defined in the imports cell. Further examples of input and output settings are available at the bottom of this notebook.
2.4 User settings#
First, we define our conversion input settings:
value_in: numerical value of input flux/mag (float)unit_in: unit or mag system for input valuewaveband_in: input’s wavelength (float) for flux, or bandpass obsmode (string) for magnitudes. The use of “waveband” here is only for the purpose of variable naming, since this can be either a wavelength or a bandpass.wavelength_unit: wavelength unit (used for plots, so needs to be specified even when using a bandpass)
value_in = 0.0
unit_in = su.VEGAMAG
waveband_in = 'johnson, v'
wavelength_unit = u.nm
Next, we define our conversion output settings:
unit_out: unit or mag system for the outputwaveband_out: wavelength (float) or bandpass obsmode (string) to find output for; if a wavelength, the unit specified in the cell above bywavelength_unitwill be used.
unit_out = su.VEGAMAG
waveband_out = 'cousins, r'
Finally, we define our spectrum to use (copy/paste from above, or define your own).
spectrum = vegaspec
3. Set up the conversion#
Now, we need to run a few cells that will set up the conversion. First, we check whether the input and output are a flux or a magnitude, and set some variables appropriately. Then, we scale the chosen spectrum such that it passes through the defined input so the extrapolation to the output wavelength will give an accurate result.
Note that the default plotting unit is set to the input unit for conversions made from flux units, and photlam for conversions from magnitudes. This may be altered, if desired, by changing the plot_unit variable definitions in the cell below.
Note: No inputs required for the cells below. All the inputs were assigned in Section 2.4.
First, let’s combine input value and unit as a quantity, then list the systems that will work for the tool.
quantity_in = value_in * unit_in
mag_systems = [u.STmag, u.ABmag, su.VEGAMAG]
flux_systems = ['spectral flux density', 'spectral flux density wav',
'photon flux density', 'photon flux density wav']
Next, let’s get inputs set up for following steps. Here are the three possible outcomes:
If the input is a magnitude,
define bandpass with input obsmode string
pivot wavelength of input bandpass
set
flux_into equivalent flux in photlam at pivot wavelength (Vega spectrum needed if using VEGAMAG)set plotting unit and flux for later
If the input is a flux,
combine wavelength for flux and unit as the input wavelength
set plotting unit and flux for later
If anything else, print
unit_in not a flux density unit or magnitude system
if unit_in in mag_systems:
mag_in = quantity_in
bandpass_in = stsyn.band(waveband_in)
wavelength_in = bandpass_in.pivot().to(wavelength_unit)
flux_in = convert_flux(wavelength_in, quantity_in, su.PHOTLAM,
vegaspec=vegaspec)
plot_unit = su.PHOTLAM
plot_flux_in = convert_flux(wavelength_in, flux_in, plot_unit)
elif unit_in.physical_type in flux_systems:
flux_in = quantity_in
wavelength_in = waveband_in * wavelength_unit
plot_unit = unit_in
plot_flux_in = convert_flux(wavelength_in, flux_in, plot_unit)
else:
print('unit_in not a flux density unit or magnitude system')
We perform a similar setup for outputs:
If the output is a magnitude,
use output wavelength to calculate output bandpass
output bandpass’s pivot wavelength
If the output is a flux,
combine wavelength for flux and unit as output wavelength
If anything else, print
unit_out not a flux density unit or magnitude system
if unit_out in mag_systems:
bandpass_out = stsyn.band(waveband_out)
wavelength_out = bandpass_out.pivot().to(wavelength_unit)
elif unit_out.physical_type in flux_systems:
wavelength_out = waveband_out * wavelength_unit
else:
print('unit_out not a flux density unit or magnitude system')
Finally, we convert the flux, scale, and multiply by our spectrum. The default evaluation unit is set to photlam.
scale = convert_flux(wavelength_in, flux_in, su.PHOTLAM) / \
spectrum(wavelength_in)
scaled_spectrum = spectrum * scale
4. Perform the conversion and create a plot#
We can now find our output by using the convert_flux function from synphot. We will first scale the spectrum defined above such that its value at the input wavelength is that of the input flux. Then, we convert the scaled spectrum’s value at the output wavelength to the selected output units, as well as the unit that will be used for plotting.
if unit_out in mag_systems:
flux_out = convert_flux(wavelength_out, scaled_spectrum(wavelength_out), unit_out,
vegaspec=vegaspec)
plot_flux_out = convert_flux(
wavelength_out, scaled_spectrum(wavelength_out), plot_unit)
else:
flux_out = convert_flux(
wavelength_out, scaled_spectrum(wavelength_out), unit_out)
plot_flux_out = convert_flux(
wavelength_out, scaled_spectrum(wavelength_out), plot_unit)
value_out = flux_out.value
Print the input and output values.
print(f'Input: {value_in:.4f} {unit_in:s} at {wavelength_in.value:.1f} {wavelength_in.unit:s}\n')
print(f'Input: {value_out:.4f} {unit_out:s} at {wavelength_out.value:.1f} {wavelength_out.unit:s}\n')
# print(f'Output: {float(value_out):.4} {} at {:.1f} {}'.format(, str(unit_out), wavelength_out.value, str(wavelength_out.unit)))
Input: 0.0000 mag(VEGA) at 547.9 nm
Input: -0.0000 mag(VEGA) at 647.3 nm
While not strictly necessary for performing the conversion, plotting the selected spectrum with the input and output points can be a useful check to see if the spectrum looks like what you’re expecting.
Let’s define a set of wavelengths and minimum/maximum bounds for the plot.
wavelength_settings = [wl.value for wl in [wavelength_in, wavelength_out]]
short = min(wavelength_settings)
long = max(wavelength_settings)
if short == long: # In case wavelength_in == wavelength_out
diff = 10.
else:
diff = long - short
right = long + diff
left = max([short - diff, 0.1])
wavelength_space = np.linspace(left, right, 10000) * wavelength_unit
We will also set the colors for the in/out markers.
if wavelength_in.value > wavelength_out.value:
c_in = 'r'
c_out = 'b'
else:
c_in = 'b'
c_out = 'r'
Plot the spectrum, input, and output. If the input was a magnitude, then plot_unit (see Section 3) will be used. In addition, if the input and output wavelength are the same, then print the input and output.
plt.figure()
# Plot spectrum
plt.plot(wavelength_space, scaled_spectrum(wavelength_space,
flux_unit=plot_unit), c='k', label='Source Spectrum')
# Plot input
plt.plot(wavelength_in.value, plot_flux_in.value,
marker='o', color=c_in, ls='none',
label='Input: {:.4} {} at {:.1f} {}'.format(
float(value_in), str(unit_in), wavelength_in.value, str(wavelength_in.unit)))
# Plot output
plt.plot(wavelength_out.value, plot_flux_out.value,
marker='s', color=c_out, ls='none',
label='Output: {:.4} {} at {:.1f} {}'.format(
float(value_out), str(unit_out), wavelength_out.value, str(wavelength_out.unit)))
# Set heights for dotted lines to markers as % of plot range
bottom, top = plt.ylim()
yrange = top - bottom
inheight = (plot_flux_in.value - bottom) / yrange
outheight = (plot_flux_out.value - bottom) / yrange
# Plot dotted lines to markers
plt.axvline(wavelength_in.to(wavelength_unit).value,
ymax=inheight, ls=':', c=c_in)
plt.axvline(wavelength_out.to(wavelength_unit).value,
ymax=outheight, ls=':', c=c_out)
# Miscellaneous
plt.ylabel('Flux ({})'.format(str(plot_unit)))
plt.xlabel('Wavelength ({})'.format(str(wavelength_unit)))
plt.legend(fontsize='small')
plt.tight_layout()
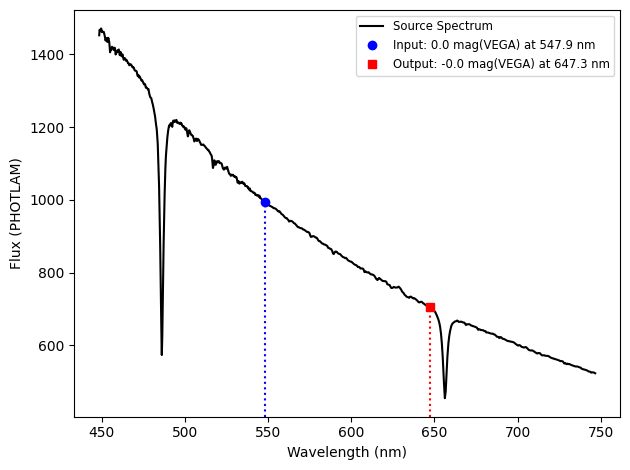
5. Examples#
Here, we provide some examples to illustrate a few of the many conversions which are possible. If desired, you may run an example cell to set the inputs for the tool, then run through the notebook (without running the cells in Section 2.4) to see the results. Each cell will define an input, output, and spectrum.
5.1. Flux in Jy to AB mag with a flat spectrum in \(F_\nu\)#
Run cell then go to Section 3 to convert flux and plot.
# Input: 3631 Jy at 550. nm
value_in = 3631.
unit_in = u.Jy
waveband_in = 550.
wavelength_unit = u.nm
# Output: Johnson V mag (AB)
unit_out = u.ABmag
waveband_out = 'Johnson, V'
# Spectrum: Flat power law in F_nu
pl_index = 0
model = PowerLawFlux1D(amplitude=flux_in, x_0=wavelength_in, alpha=pl_index)
spectrum = SourceSpectrum(model)
5.2. Flux in flam to Flux in flam along a blackbody#
Run cell then go to Section 3 to convert flux and plot.
# Input: 1.234e-8 flam at 500. nm
value_in = 1.234e-8
unit_in = su.FLAM
waveband_in = 500.
wavelength_unit = u.nm
# Output: flam at 800. nm
unit_out = su.FLAM
waveband_out = 800.
# Spectrum: 5800 K blackbody
bb_temp = 5800 * u.K
model = BlackBody1D(bb_temp)
spec = SourceSpectrum(model)
5.3. Flux in fnu to flux in photnu, any spectrum (same wavelength)#
Run cell then go to Section 3 to convert flux and plot. Note the spectrum is irrelevant since conversion is at the same wavelength.
# Input: 1.234e-21 fnu at 686. nm
value_in = 1.234e-21
unit_in = su.FNU
waveband_in = 686.
wavelength_unit = u.nm
# Output: photnu at 686. nm
unit_out = su.PHOTNU
waveband_out = 686.
# Spectrum: 5800 K blackbody
bb_temp = 5800 * u.K
model = BlackBody1D(bb_temp)
spectrum = SourceSpectrum(model)
5.4. mag to mag from an HST bandpass to a Johnson bandpass, flat spectrum in \(F_\lambda\)#
Run cell then go to Section 3 to convert flux and plot. Note we run convert_flux for the power law amplitude to ensure the spectrum is flat in \(F_\lambda\) rather than in photlam.
# Input: STmag = 12.240, F606W filter on WFC3 UVIS 2
value_in = 12.240
unit_in = u.STmag
waveband_in = 'wfc3, uvis2, f606w, mjd#59367'
wavelength_unit = u.nm
# Output: Johnson V mag (AB)
unit_out = u.STmag
waveband_out = 'Johnson, V'
# Spectrum: Flat power law in F_lambda
pl_index = 0
model = PowerLawFlux1D(amplitude=convert_flux(
606 * u.nm, 1., su.FLAM), x_0=606 * u.nm, alpha=pl_index)
spec = SourceSpectrum(model)
model = PowerLawFlux1D(amplitude=flux_in, x_0=wavelength_in, alpha=pl_index)
6. Conclusions#
Thank you for walking through this notebook. Now using WFC3 data, you should be more familiar with:
Performing conversions between various systems of flux and magnitude using the
synphotandstsynphotpackages.Extrapolating an output flux at a different wavelength than the input flux.
Adapting a more personalized and streamlined conversion process.
Congratulations, you have completed the notebook!#
Additional Resources#
Below are some additional resources that may be helpful. Please send any questions through the HST Helpdesk.
-
see sections 9.5.2 for reference to this notebook
About this Notebook#
Authors: Aidan Pidgeon, Joel Green; WFC3 Instrument Team
Updated on: 2021-09-13
Citations#
If you use numpy, astropy, synphot, or stsynphot for published research, please cite the
authors. Follow these links for more information about citing the libraries below:
Top of Page
